一、什么是“平衡二叉查找树”
平衡二叉树的严格定义是这样的:二叉树中任意一个节点的左右子树的高度相差不能大于 1。完全二叉树、满二叉树都是平衡二叉树,但是非完全二叉树也有可能是平衡二叉树。
平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
二、红黑树
红黑树,Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST)。
一.红黑树的定义
合格的红黑树需要满足以下几个要求
1、 根节点是黑色的(树顶是黑色的);
2、 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据(树根是黑色的,所有结点的叶子节点都是黑色的,但是黑色的并不都是叶子节点,叶子节点不存储数据);
3、 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;(红色节点的父亲一定不能是红色节点,但是黑色节点的父亲可以是黑色节点);
4、 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点(这个其实可以用一张图来表示,一棵红黑树,在去掉所有红节点之后剩下的黑节点是等高的);
要求2图解
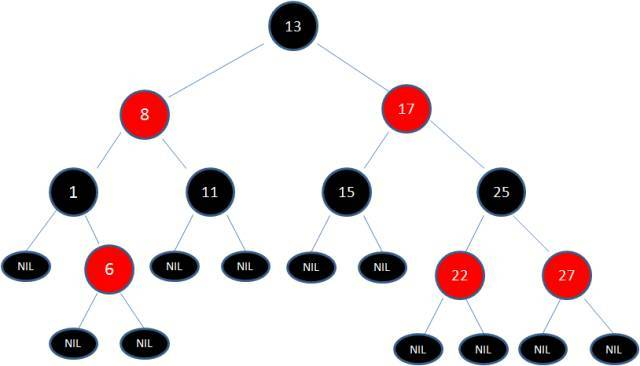
要求4图解
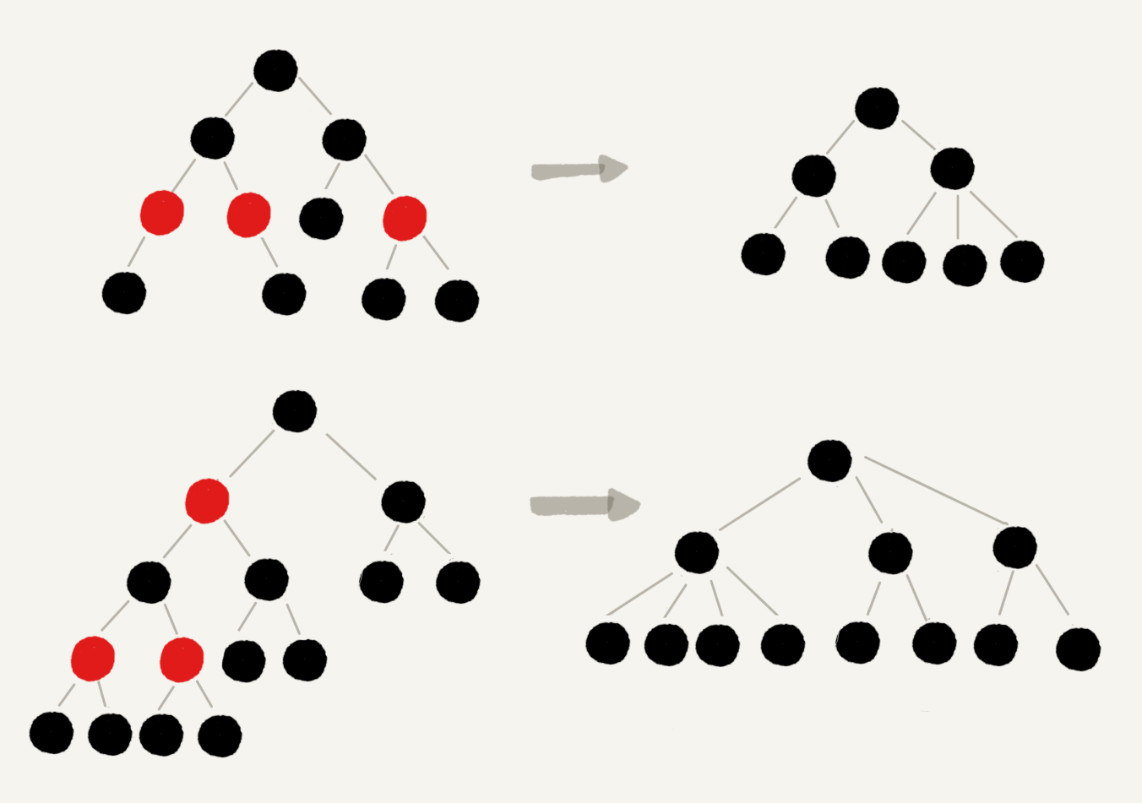
二.红黑树的平衡操作
1、旋转操作(使树达到平衡的关键操作)
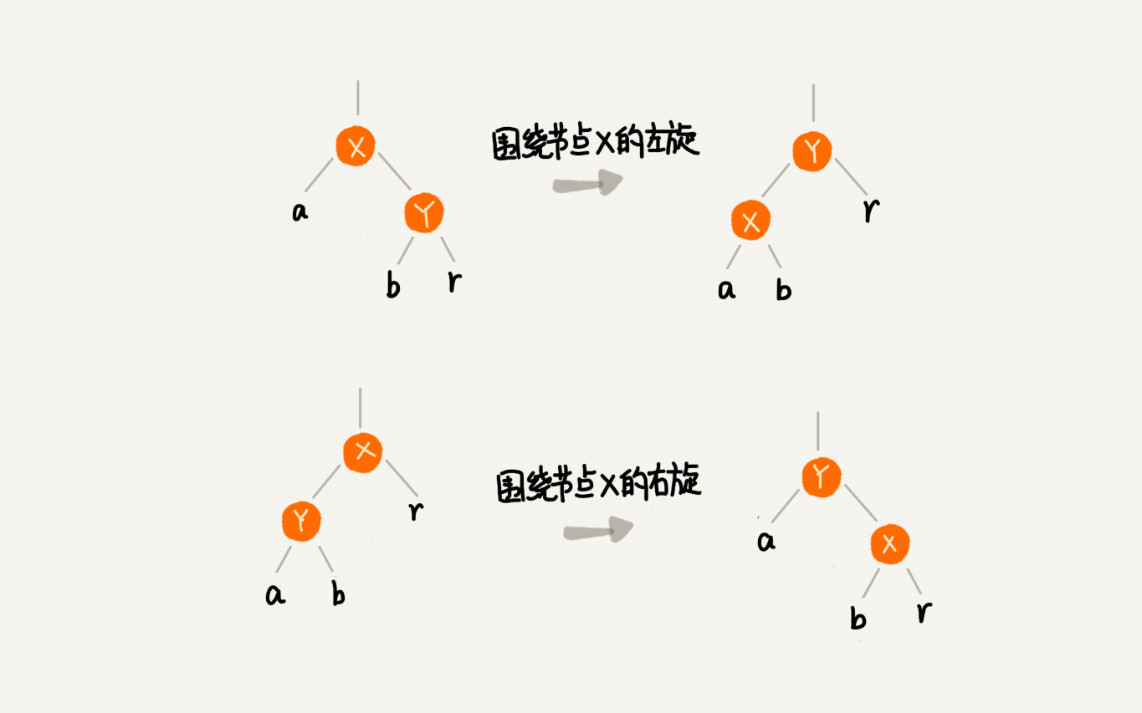
对于树结构,A<Y<B<X<R,左侧数据小于右侧数据,在这个的前提下,发生未知的转变。
1.左旋(rotate left)
左旋操作是将X节点变为右子节点的左子节点,并且把右子节点的左子节点变为围绕点的右子节点(好绕口)
2.右旋(rotate right)
右旋操作是指将X节点变为自己左子节点的右子节点,并且把右子节点的右子节点变为X的左子节点。(同绕口)
2、变色(重新标记节点为黑色或红色)
红黑树规定,插入的节点必须是红色的。而且,二叉查找树中新插入的节点都是放在叶子节点上。
就是因为有了插入或者删除操作,所以才会影响到树的平衡性,因为插入了不同的红色节点,才会需要进行变色。
三.红黑树的插入操作
红黑树规定,插入的节点必须是红色的。
1、父为黑色
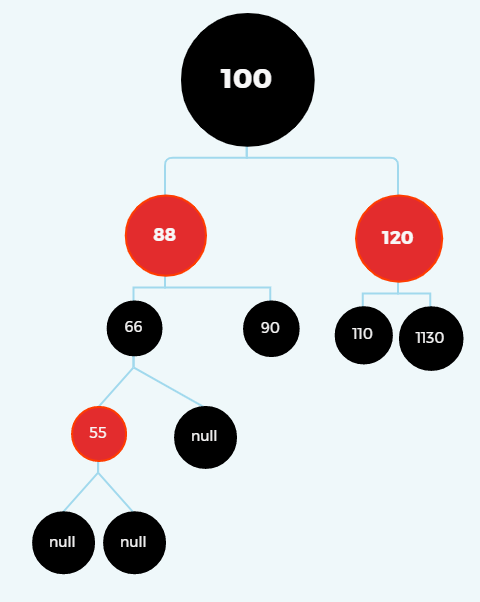
55为插入值,直接插入,无需任何操作,原来树本身就是稳定结构,也不需要进行旋转。
2、父为红色
1.叔叔是红色
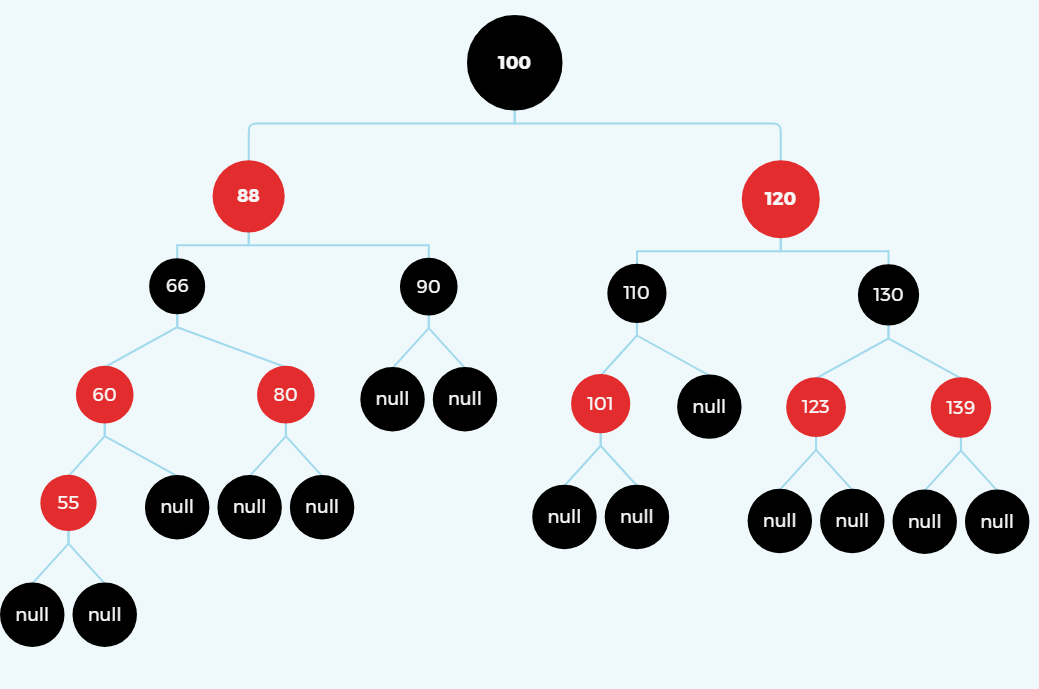
这块比较难理解,因为有一个思维的误区。
在插入55后,首先要将60和80变为黑色,将66变为红色。
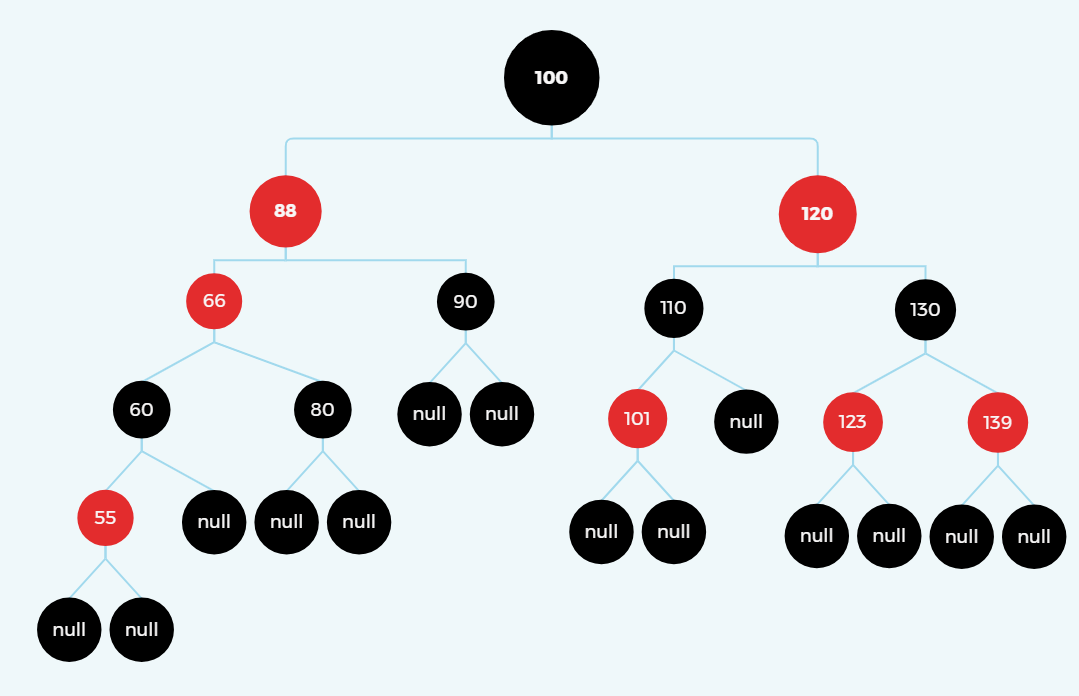
此时的情况比较复杂,66和88都是红色,100是黑色。
有两个问题
1、 根节点100只能是黑色;
2、 如果把88改为黑色,此时红黑树就失去了平衡;
因此,这里单纯的去改变颜色,已经不能满足需求了,需要改变颜色并且进行旋转操作。
此时以根节点为中心,左右两侧区分,左侧增加了新的黑色节点,打破了原有的平衡,需要进行右旋。

右旋操作是指将X节点变为自己左子节点的右子节点,并且把右子节点的右子节点变为X的左子节点。
此时把80看作是X,66看作是Y,进行右旋。
a=60,b=80,Y=60,X=66,r=80
a、b为Y的左右子节点,Y为X的左子节点,r为X的右子节点。
围绕X右旋之后X变为Y的右子节点,b变为X的左子节点。
旋转后如图所示
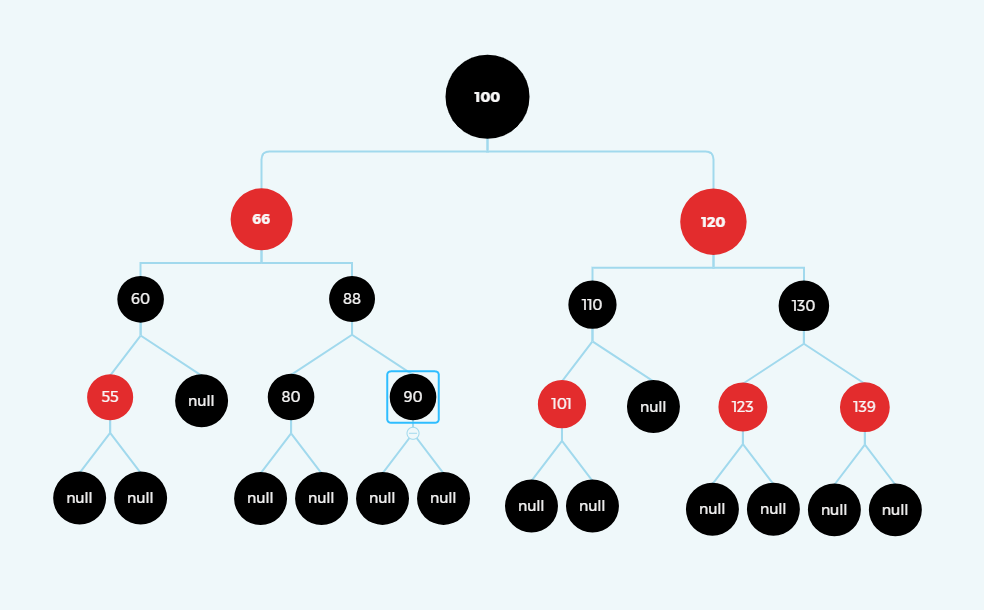
此时的红黑树并没有达到红黑树的标准,因为100,88,80黑色节点为三层,而其他的都为两层,需要重新变色,看80和90节点,其父节点为黑色,只需要将80和90变为红色即可。
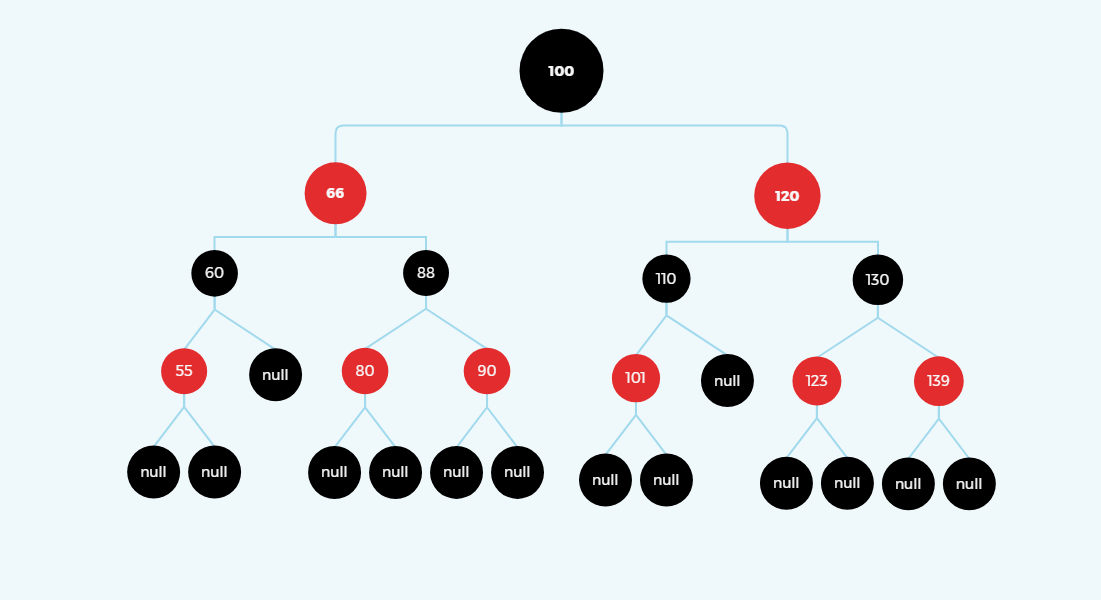
此时得到的是一个平衡的红黑树。
2.叔叔是黑色
(1).爸爸在左、叔叔在右、我在左
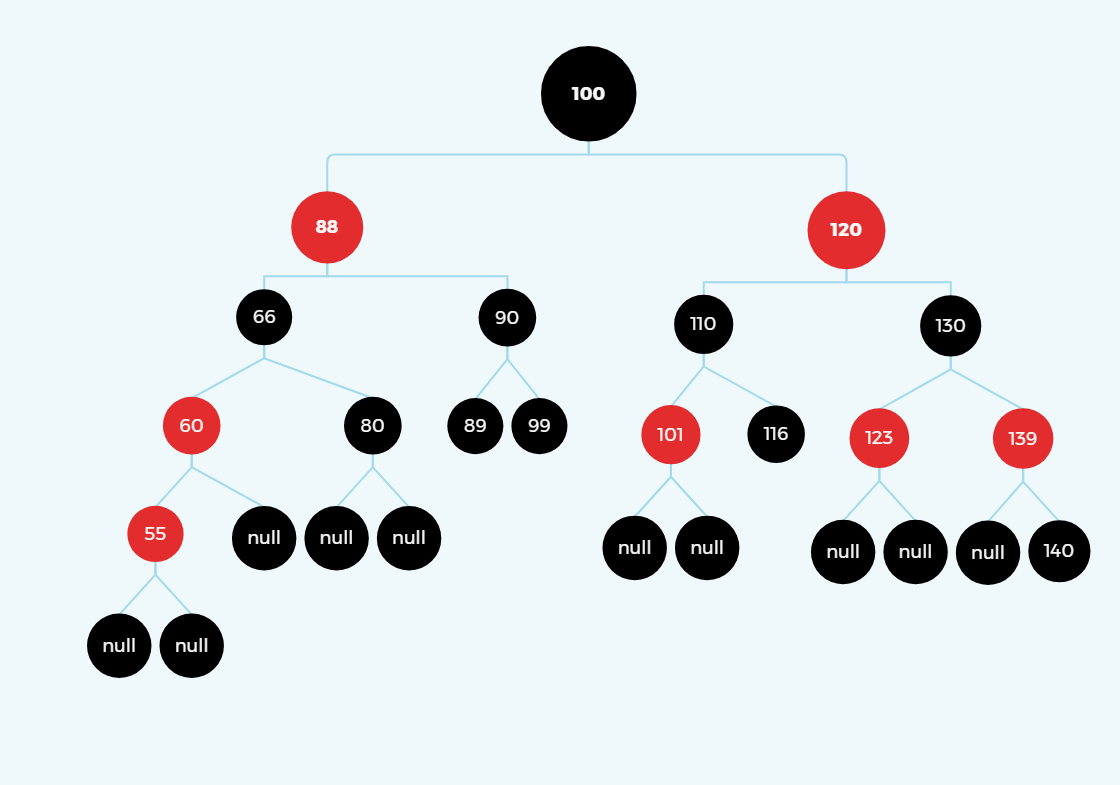
之前画的图因为不是标准的红黑树,最开始我的理解有一点问题,因此这个图我重新画了。
现在是标准的三层黑色红黑树,插入55
变色
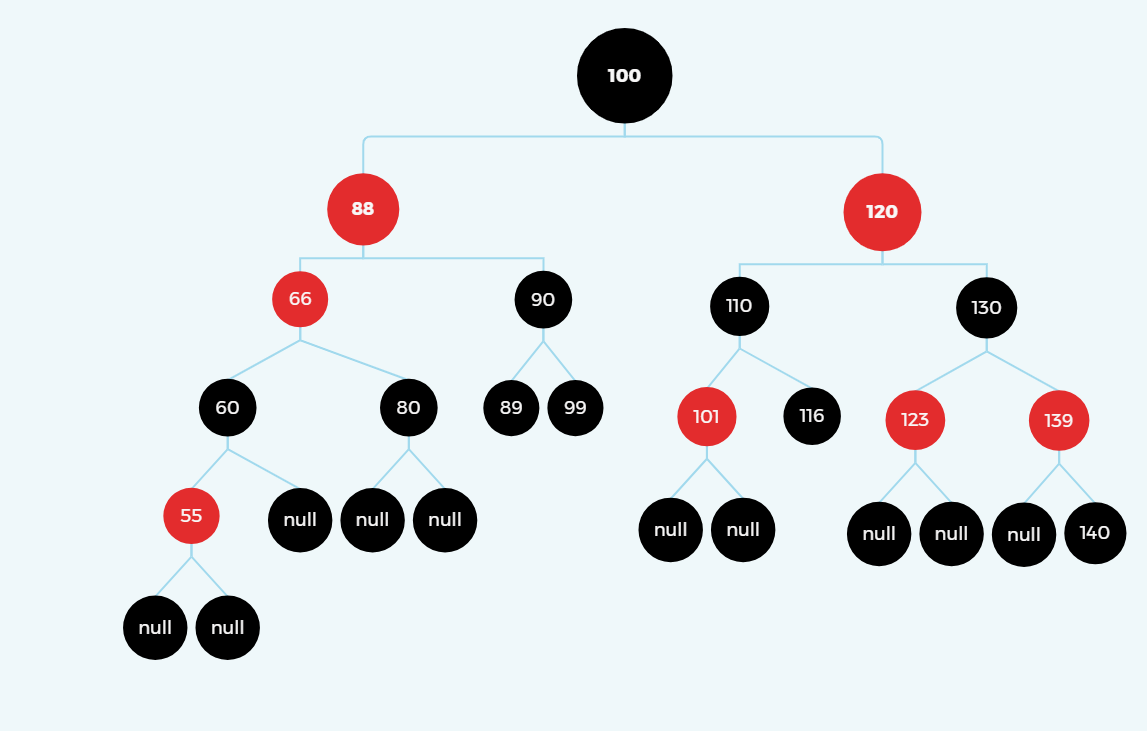
以66为X目标点,60为Y进行右旋转
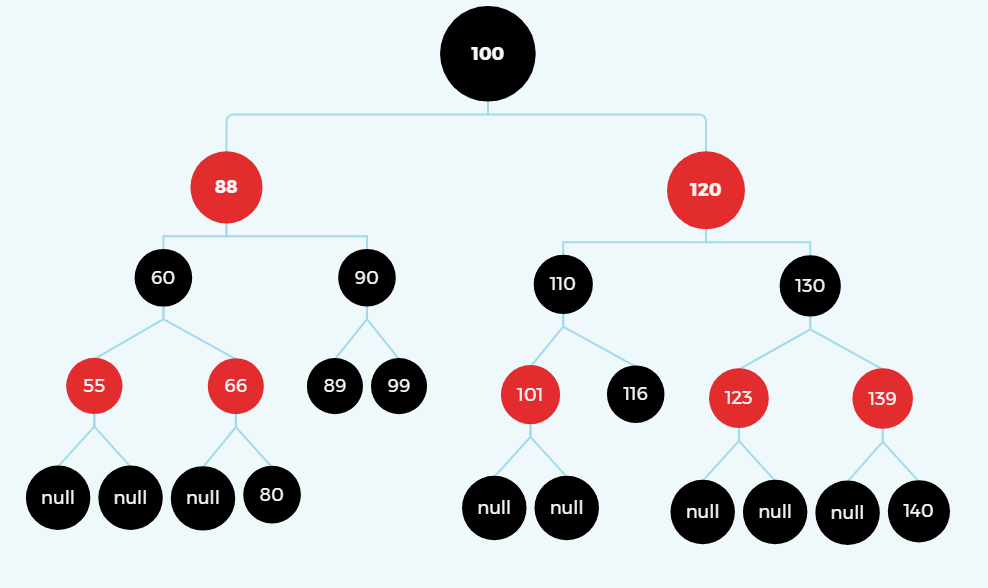
(2).爸爸在左、叔叔在右、我在右
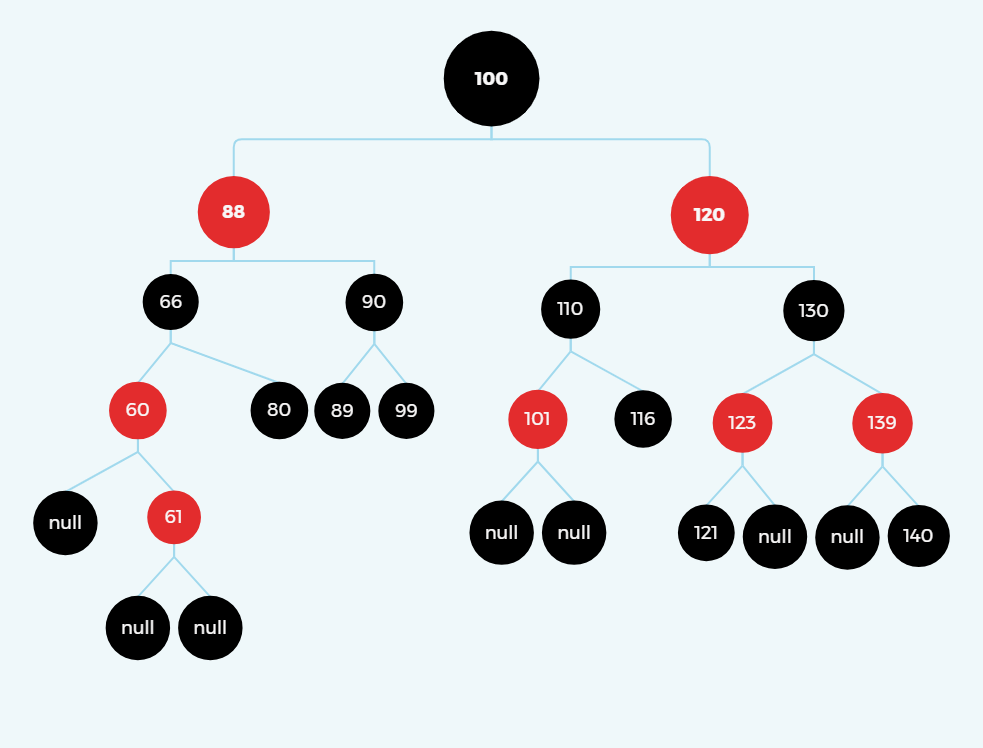
变色
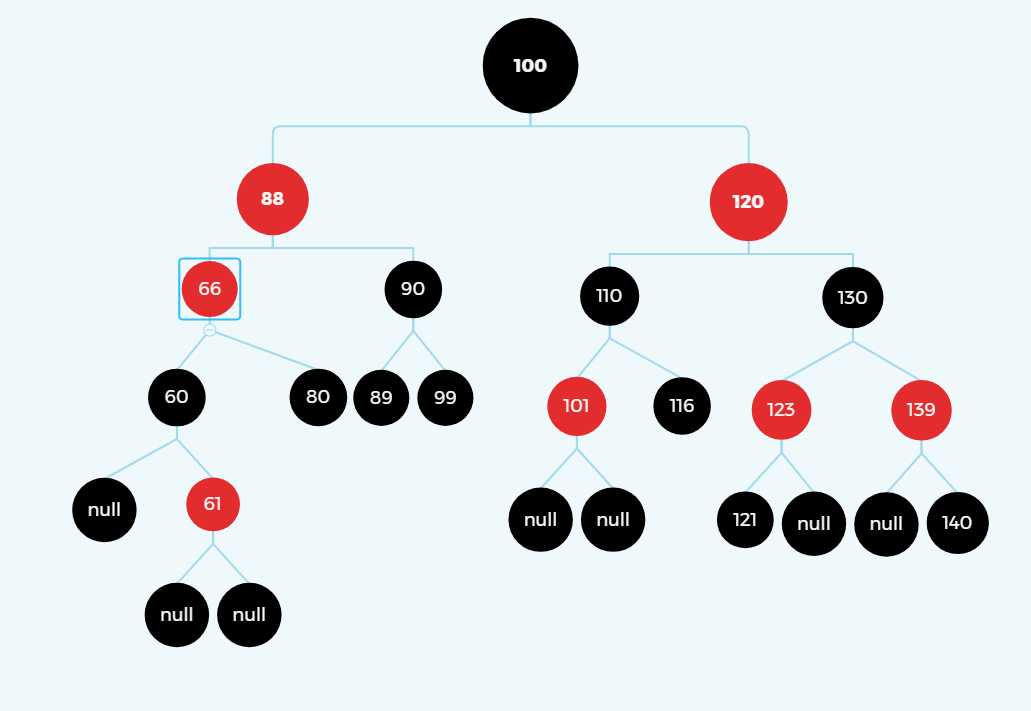
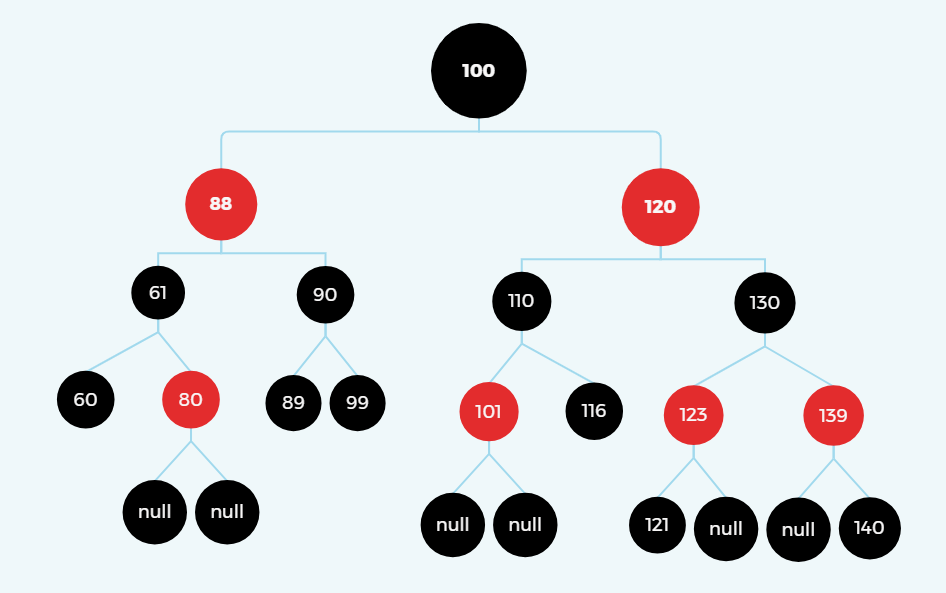
旋转(右旋)
(3).叔叔在左、爸爸在右、我在左
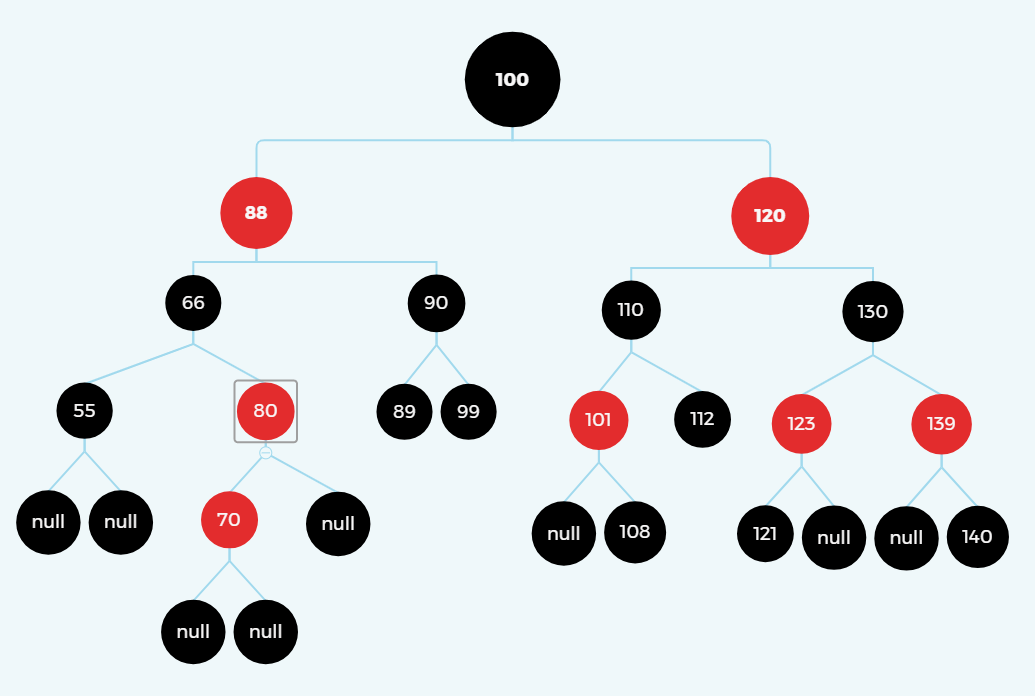
变色
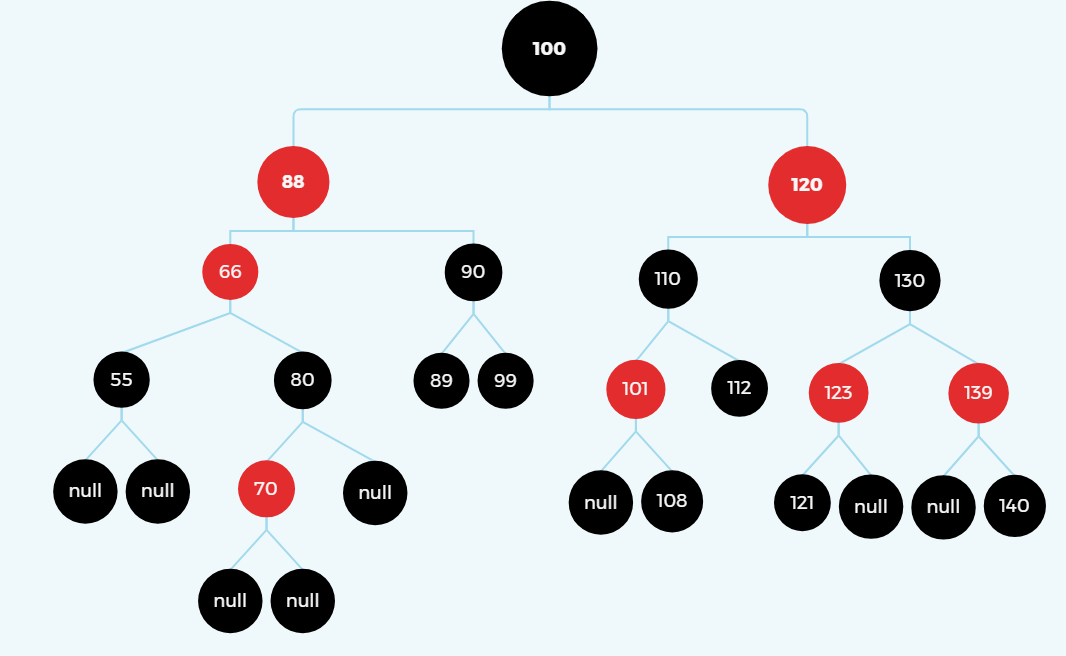
旋转(左旋)
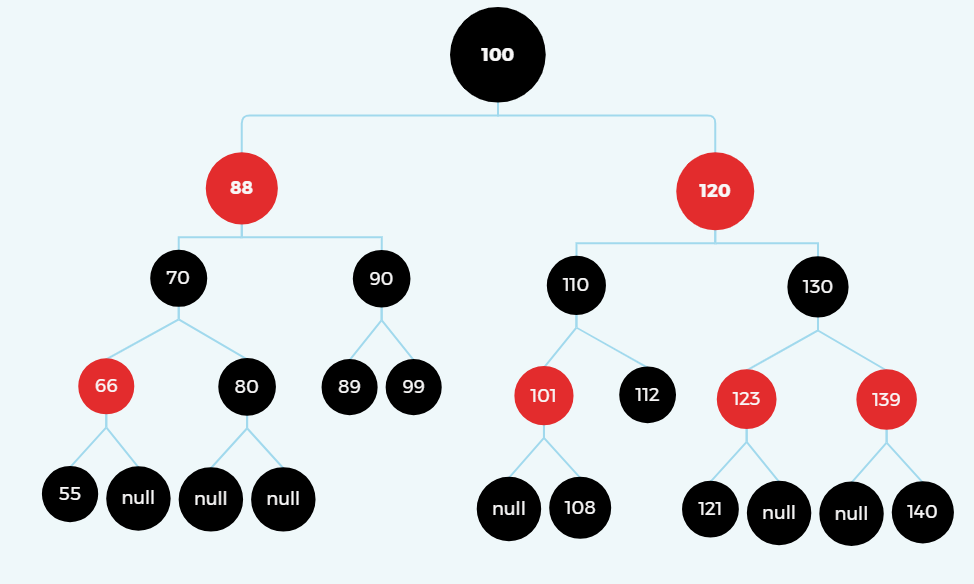
(4).叔叔在左、爸爸在右、我在右
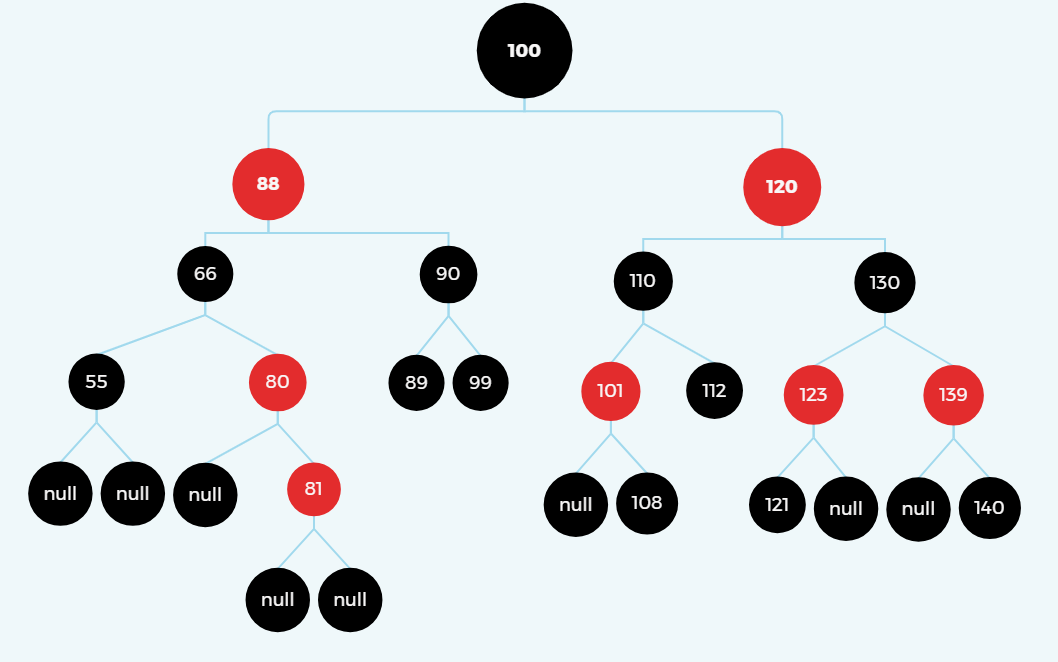
变色
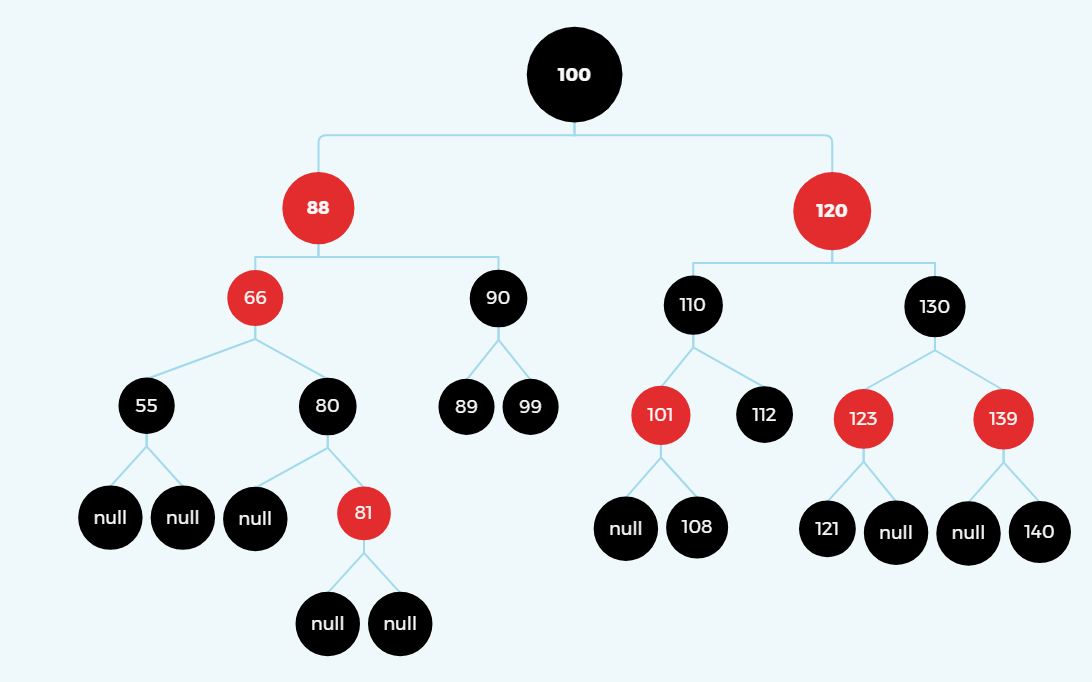
旋转
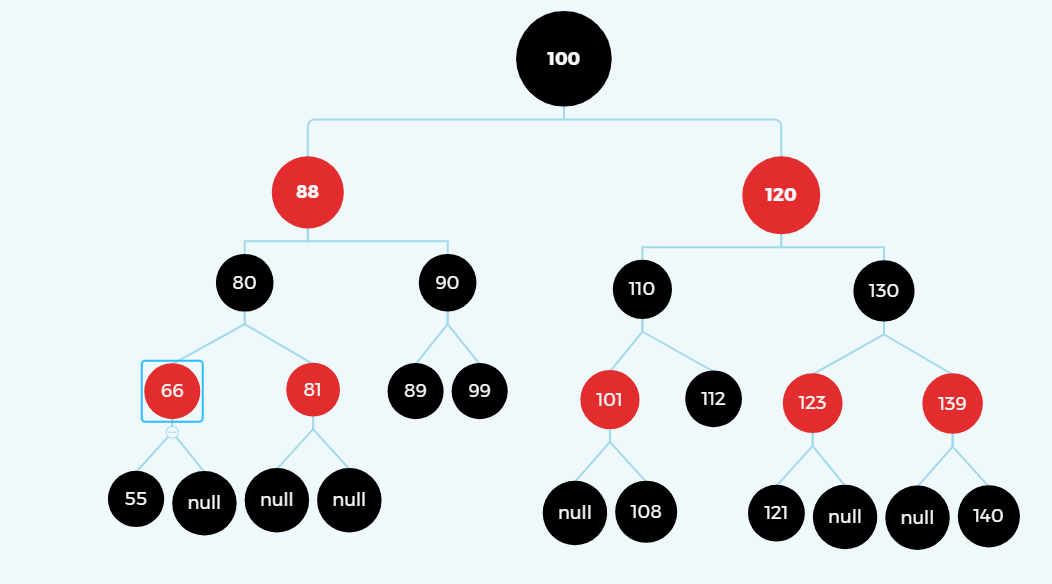
四.红黑树的删除操作
之前用的是一个很糟糕脑图软件,今天换了一个,这个一下子好看了很多。
开始讨论删除的情况,在我看来删除操作主要考虑的是原有树结构失衡。
删除操作的平衡调整分为两步:
第一步是针对删除节点初步调整。初步调整只是保证整棵红黑树在一个节点删除之后,仍然满足最后一条定义的要求,也就是说,每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;(删除)
第二步是针对关注节点进行二次调整,让它满足红黑树的第三条定义,即不存在相邻的两个红色节点。(变色旋转)
1、删除操作
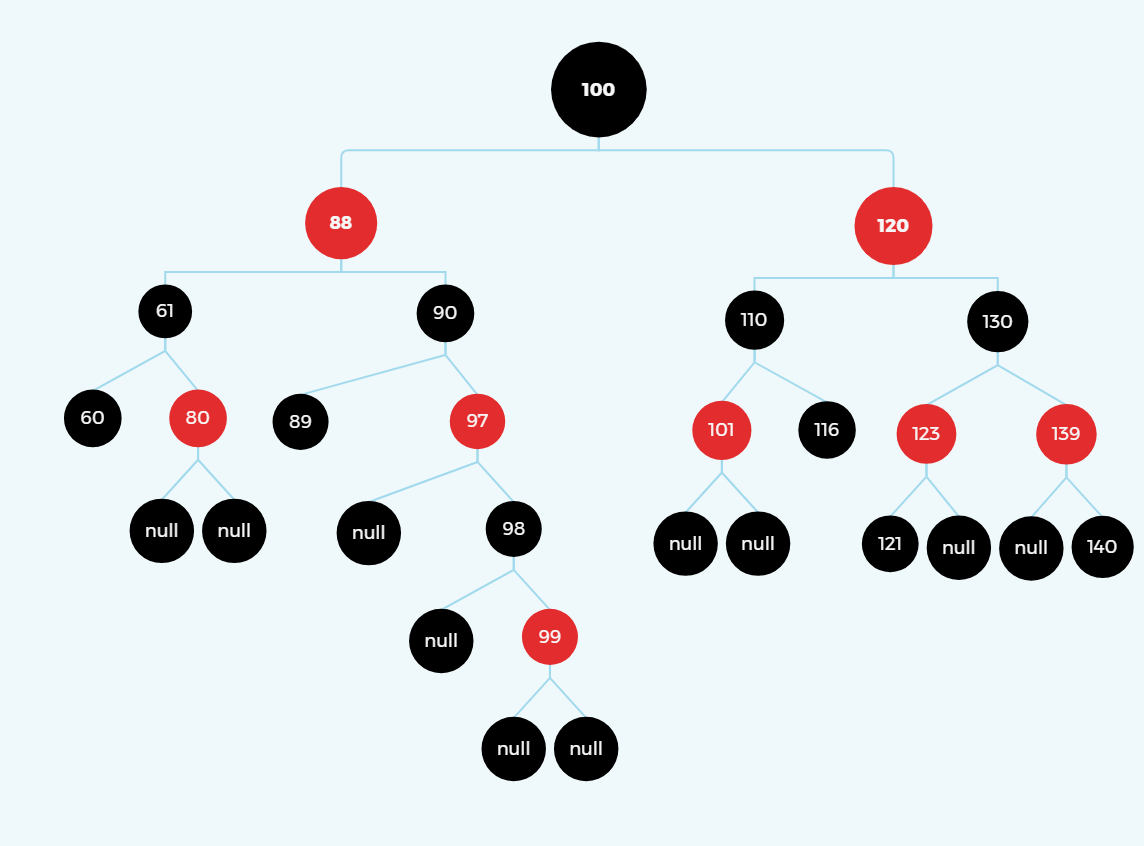
1.被删除节点没有子节点
直接删除,比如删除121或者140
2.被删除节点只有一个非空子节点
子节点顶替删除节点位置,这里有一个颜色的区分
(1).删除节点的颜色是黑色的(对平衡有影响)
比如删除的是98,需要用99去顶替,顶替之后99需要进行变色,变色为黑色
(2).删除节点的颜色是红色的(对平衡无影响)
删除红色其实对平衡性没有任何影响,比如删除的是97,可以用98顶上去。
3.被删除节点有两个非空节点
对于普通的二叉树来讲,删除一个有两个子节点的结点的时候,需要用前驱节点或者后继节点来进行替代。
以88举例
前驱节点是小于88的最大值:80
后继节点是大于88的最小值:89
我在B站看到一个视频,我觉得这个大佬的思路很棒,我很喜欢,视频链接。
对于红黑树和二叉查找树都适用。
现在的情况是要去删除拥有两个子节点的节点。
我按照我画的图举几个例子,主要的思想是替换,可以比别的思路少很多步骤。
(1).删除的节点是100
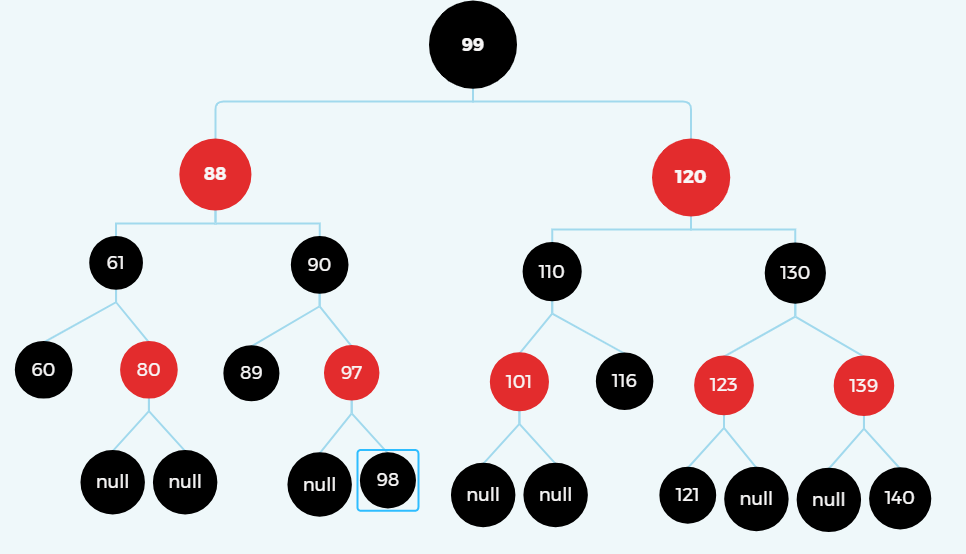
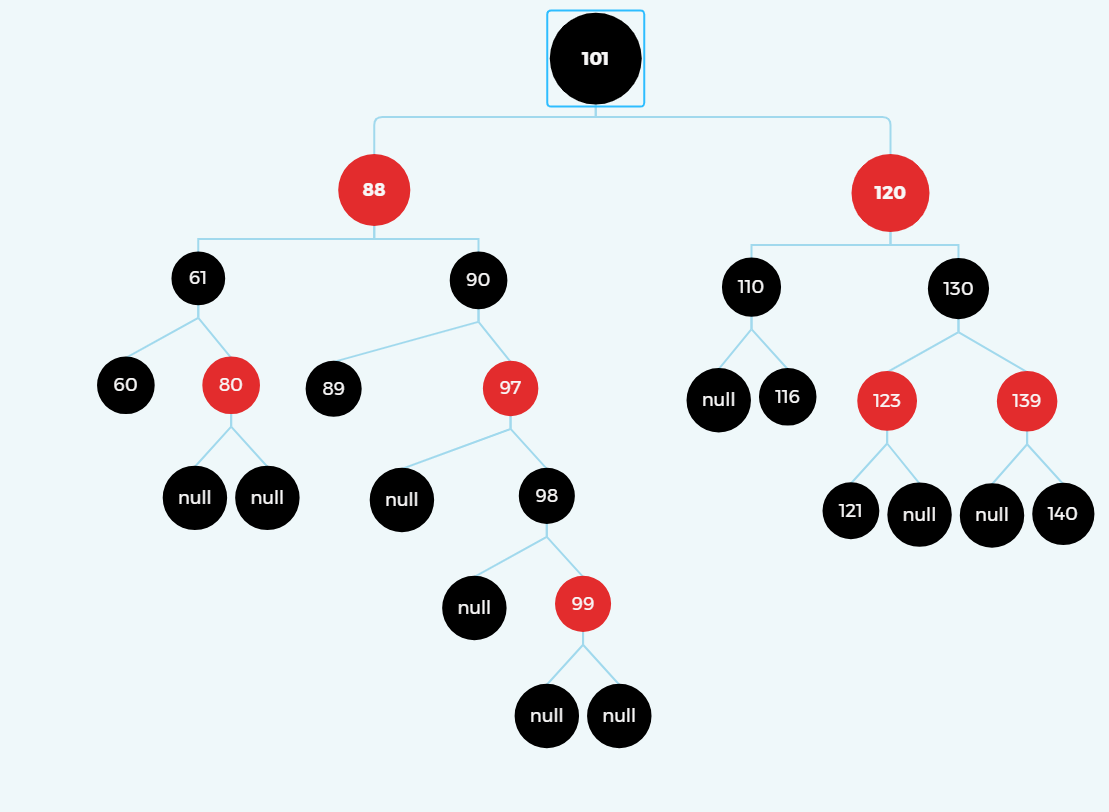
100为根节点,拥有两个子节点,删除一个有两个子节点的结点的时候,需要用前驱节点或者后继节点。
100的前置节点是99,后置节点是101。
这里其实有一个小小的技巧性,因为对于一个要被删除的节点,
它的前置节点必然只有以下两种情况:
(1)没有子节点
(2)只有一个左子节点
它的后置节点必然只有以下两种情况:
(1)没有子节点
(2)只有一个右子节点
因为如果前置节点有了右子节点那么前置节点肯定不是比被删除节点小的最大值。
后置节点同理。
比如删除100,可以用99去替换100,并且替换之后保持被删除节点位置的颜色不变,并且将99这个节点删掉,99删掉之后完全没有影响二叉树的平衡。
(2).删除的节点是120
100的前置节点是116,后置节点是121。
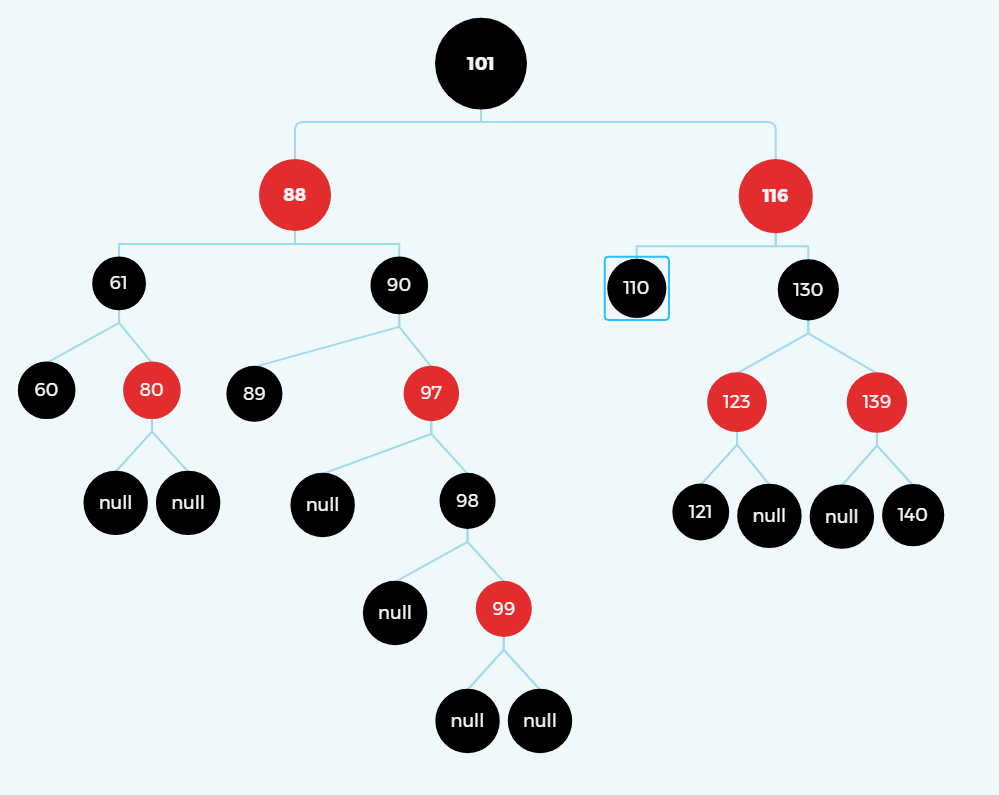
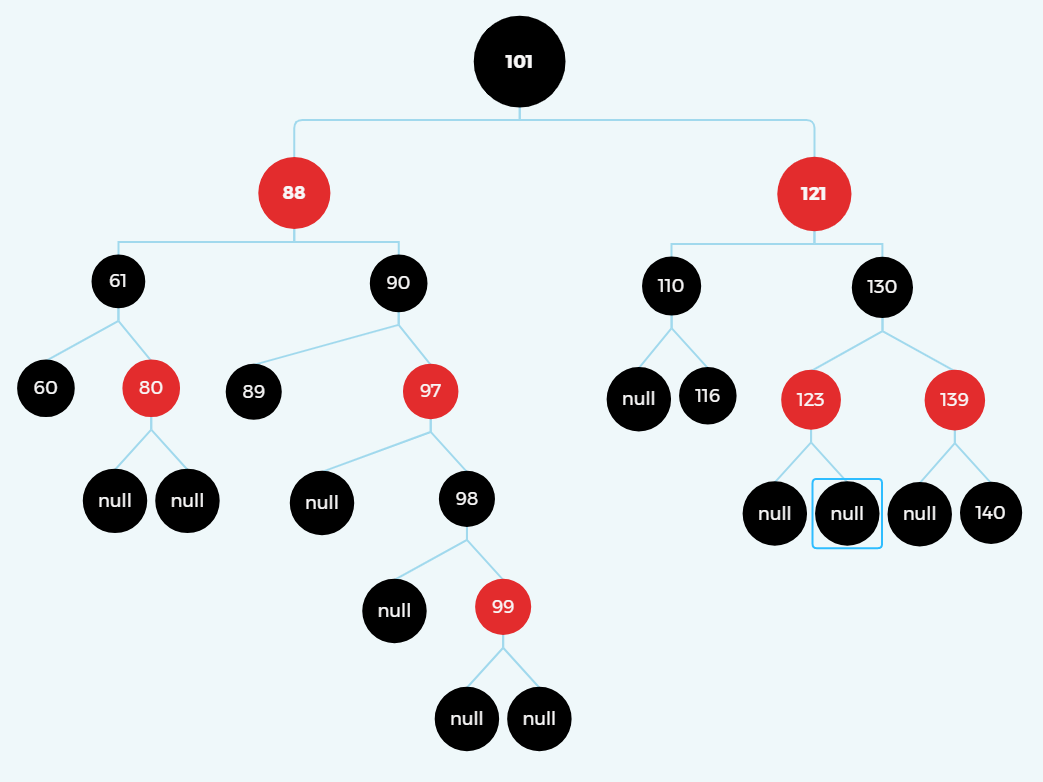
这样是不是极大的简化了思维,并且保证了红黑树的平衡性。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: