一、什么是排序
所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。
二、怎么分析一个排序算法
一.排序算法的执行效率
1、最好情况，最坏情况，平均情况时间复杂度分析
为什么要区分这三种时间复杂度呢？第一，有些排序算法会区分，为了好对比，所以最好都做一下区分。第二，对于要排序的数据，有的接近有序，有的完全无序。有序度不同的数据，对于排序的执行时间肯定是有影响的，要知道排序算法在不同数据下的性能表现。
2、时间复杂度的系数、常数 、低阶
对于不同规模的数据，排序算法的性能不同。
3、比较次数和交换（或移动）次数
基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，如果在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。
4、有序度和逆序度
有序度是数组中具有有序关系的元素对的个数。
逆序度的定义正好跟有序度相反（默认从小到大为有序）
逆序度 = 满有序度 - 有序度
比如一个数组[0,1,2,3,4,5,6,7,8,9]，从小到大排列，这个就是完全有序的数组，有序度是9+8+…+3+2+1=N*(N-1)/2=45
二.排序算法的内存消耗
算法的内存消耗可以通过空间复杂度来衡量
三.排序算法的稳定性
仅仅用执行效率和内存消耗来衡量排序算法的好坏是不够的。针对排序算法，还有一个重要的度量指标，稳定性。这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。
三、常见排序算法
| 排序算法 | 是否原地排序 | 是否稳定 | 最好 | 最坏 | 平均 | 适用于 |
|---|---|---|---|---|---|---|
| 冒泡排序 | 是 | 是 | O(N) | O(N^2) | O(N^2) | 小数据量 |
| 插入排序 | 是 | 是 | O(N) | O(N^2) | O(N^2) | 小数据量 |
| 选择排序 | 是 | 否 | O(N^2) | O(N^2) | O(N^2) | 小数据量 |
| 归并排序 | 否 | 是 | O(NlogN) | O(NlogN) | O(NlogN) | 大数据量 |
| 快速排序 | 是 | 否 | O(NlogN) | O(N^2） | O(NlogN) | 大数据量 |
| 桶排序 | 否 | 不一定，看桶内排序 | O(N) | O(NlogN) | O(N) | 特定数据类型 |
| 计数排序 | 是 | 否 | O(N) | O(NlogN) | O(N) | 特定数据类型 |
| 基数排序 | 是 | 是 | O(DN) | O(DN) | O(DN) | 位排序 |
一.冒泡排序（Bubble Sort,适合较小规模数据排序）
冒泡排序是进行循环比较，每次对比的是第X个元素和第X+1个元素的大小（X及X+1小于元素总数N）
如果不满足大小关系需求，则进行数据交换，一次冒泡至少会让一个元素移动到它该存在的位置。
1、冒泡排序代码
// 冒泡排序，a表示数组，n表示数组大小
public void bubbleSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 0; i < n; ++i) {
// 提前退出冒泡循环的标志位
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j) {
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true; // 表示有数据交换
}
}
if (!flag) break; // 没有数据交换，提前退出
}
}
2、冒泡排序是原地排序算法吗？
冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O(1)，是一个原地排序算法。
3、冒泡排序是稳定的排序算法吗？
在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法。
4、冒泡排序的时间复杂度是多少？
冒泡排序包含两个操作原子，比较和交换。每交换一次，有序度就加 1。不管算法怎么改进，交换次数总是确定的，即为逆序度，也就是n*(n-1)/2–初始有序度。
对于包含 n 个数据的数组进行冒泡排序，平均交换次数是多少呢？最坏情况下，初始状态的有序度是 0，所以要进行 n*(n-1)/2 次交换。最好情况下，初始状态的有序度是 n*(n-1)/2，就不需要进行交换。可以取个中间值 n*(n-1)/4，来表示初始有序度既不是很高也不是很低的平均情况。
这种算法不严格，但是其实挺好用的，因为根据实际数据通过概率论去分析数据太过复杂，不如取个期望值进行计算。
二.插入排序（Insertion Sort,适合较小规模数据排序）
一个有序的数组，往里面添加一个新的数据后，如何继续保持数据有序呢？只要遍历数组，找到数据应该插入的位置将其插入即可，这个思路就是插入排序。
插入排序具体是如何借助上面的思想来实现排序的呢？
首先将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。
插入排序的核心思想是将数据分成两部分，第一部分是已排序部分，第二部分是未排序部分。最开始设置INDEX(0)为已排序部分，然后再和INDEX(1)进行比较。
以下面的数组为例：4，5，6，1，3，2。
初始已排序是：4，未排序是5，6，1，3，2。
4和5进行比较后，已排序部分是4，5。未排序部分是6，1，3，2。
第三次，6和4，5进行比较之后（会和4和5都进行比较），已排序部分是4，5，6。未排序部分是1，3，2。
第四次，1和4，5，6进行比较（和4进行比较），比较之后就插在了456之前。
…
1、插入排序的代码
// 插入排序，a表示数组，n表示数组大小
public void insertionSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 1; i < n; ++i) {
int value = a[i];
int j = i - 1;
// 查找插入的位置
for (; j >= 0; --j) {
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}
}
a[j+1] = value; // 插入数据
}
}
2、插入排序是原地排序算法吗？
从实现过程可以很明显地看出，插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O(1)，也就是说，这是一个原地排序算法。
3、插入排序是稳定的排序算法吗？
在插入排序中，对于值相同的元素，可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。
4、插入排序的时间复杂度是多少？
对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行 n 次插入操作，所以平均时间复杂度为 O(n^2)。
三.选择排序（Selection Sort,适合较小规模数据排序）
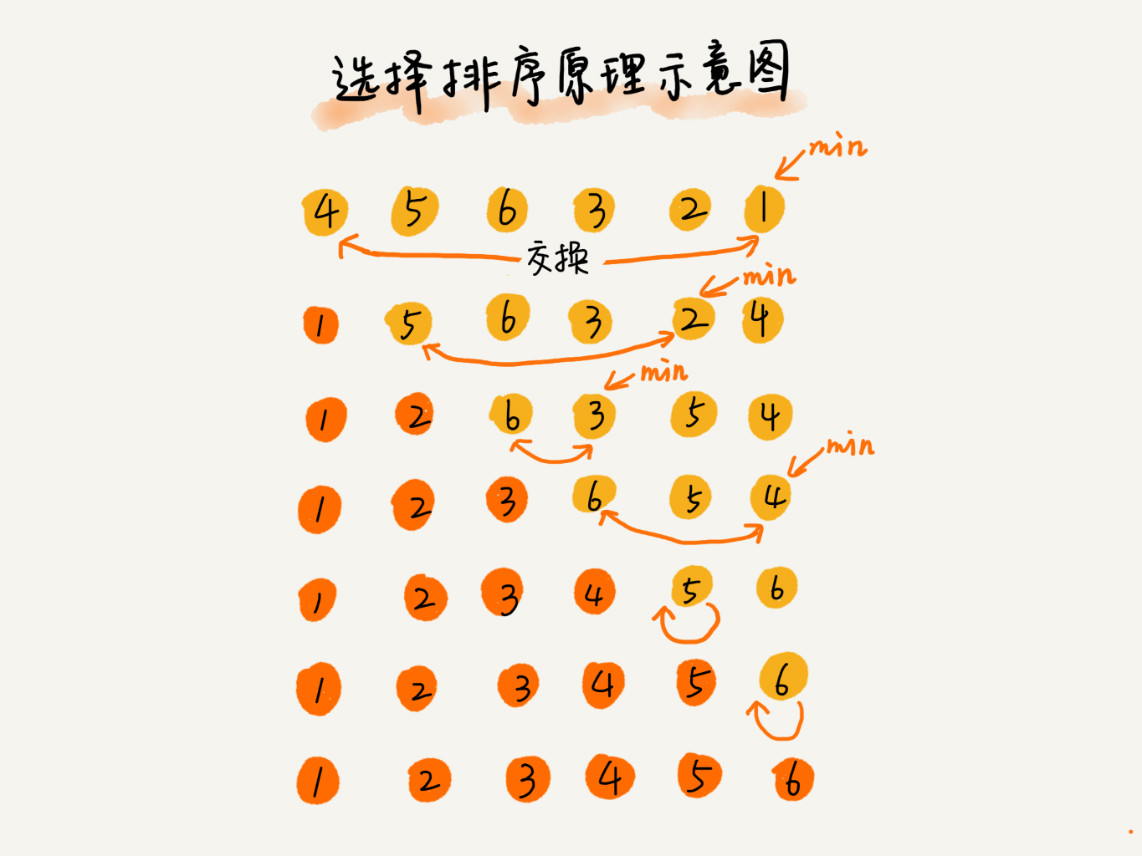
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。
选择排序
比如有N个元素，会在N个元素中先去找最小的元素，然后将最小的元素和INDEX（0）的元素进行交换，之后再在N-1个元素里找最小的元素，一直找到最后一个。
1、选择排序的代码
public class SelectSort {
public static void main(String[] args) {
int [] arr = {
49,38,65,97,76,13,27,49};
selectSort(arr,arr.length);
}
public static void selectSort(int [] arr,int n){
for (int i = 0; i < n - 1; i++) {
int index = i;
int j;
// 找出最小值得元素下标
for (j = i + 1; j < n; j++) {
if (arr[j] < arr[index]) {
index = j;
}
}
int tmp = arr[index];
arr[index] = arr[i];
arr[i] = tmp;
System.out.println(Arrays.toString(arr));
}
}
}
2、选择排序是原地排序算法吗？
选择排序空间复杂度为 O(1)，是一种原地排序算法。
3、选择排序是稳定的排序算法吗？
选择排序并不是稳定的排序算法，比如数据时5，6，5，7，8，9，1。
第一次循环查找最小数据的时候，会将1和第一个5进行交换，这样，两个相同的5的前后顺序就发生了变化，因此不是稳定的个排序算法。
4、选择排序的时间复杂度是多少？
选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n^2)
四.归并排序（Merge Sort，适合大规模数据排序，比较难理解）
归并排序的核心思想不复杂，是将需要排序的数组，从中间进行拆分，然后对前后两部分分别进行排序，如果还可以进行拆分那么再进行拆分和排序。一直拆到两个元素为一对，然后通过对比在进行排序，两组已排序好的两个元素再进行对比排序。
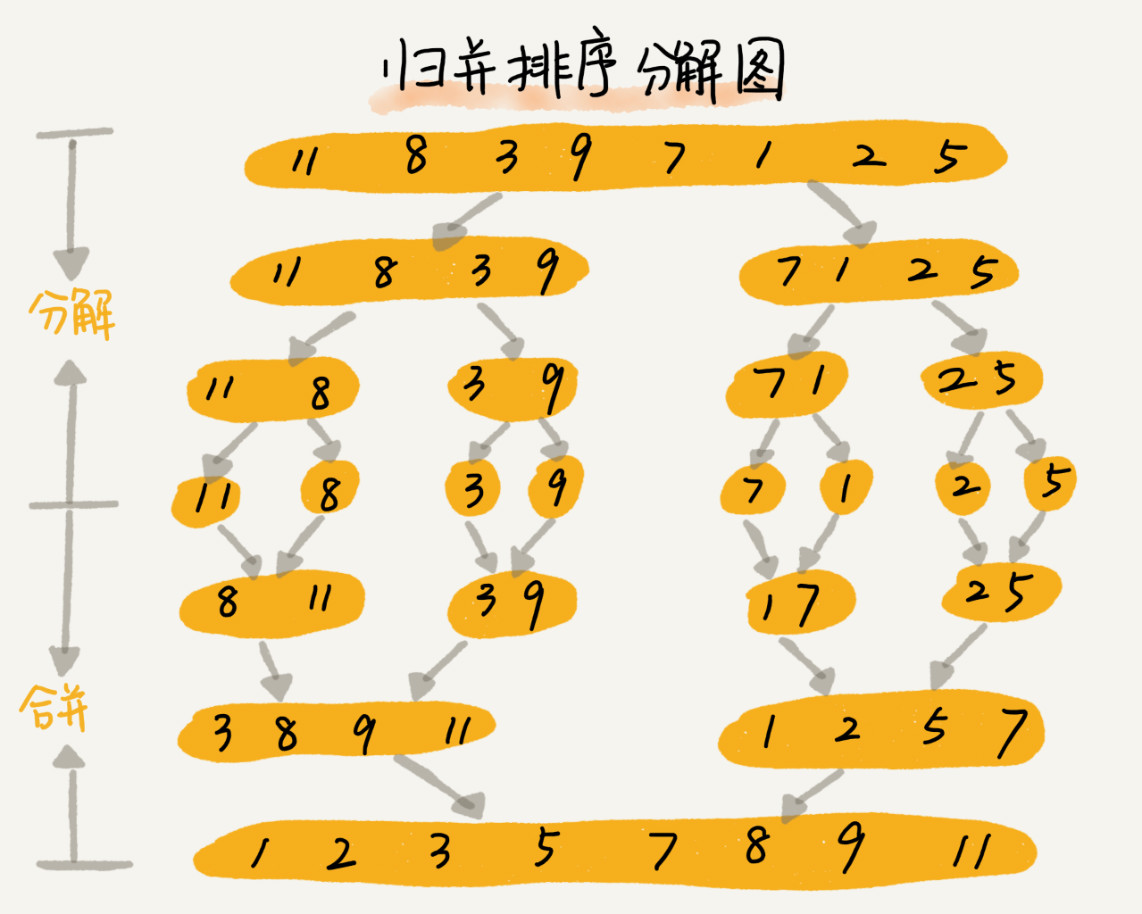
下面是大佬给出的另一个例子（临时数据为局部变量），图描述的是根据指针来合并两个已经排好顺序的数组，将其合并为一个数组，我按照这个思路描述一下上面的。
首先申请一个临时数组（可以为局部变量也可以为全局变量，此时代码中设置的是局部变量，此时假定为全局变量），将数组{11，8，3，9，7，1，2，5}（8个元素，长度为7），先是将其拆分为两个数组{11，8，3，9}和{7，1，2，5}（这个地方并不是实际的拆分为两个数组，而是根据下标数，将其一分为二。）。
再将这两个数组分别拆分为{11，8}，{3，9}，{7，1}，{2，5}，当发现无法再进行细化拆分的时候，数组中元素进行比较，从小到大排序，则得出以下四个数组{8，11}，{3，9}，{1，7}，{2，5}，此时为第一次排序，然后对{8，11}和{3，9}，及{1，7}，{2，5}进行合并。
（1）是对下标[0,1]进行排序
对{11，8}进行排序时，临时数组为{8,11,0,0,0,0},排序完成之后将数据赋值给原数组，原数组变为为{8，11，3，9，7，1，2，5}。
（2）是对下标[2,3]进行排序
对{11，8}进行排序时，临时数组为{8,11,3,9,0,0},排序完成之后将数据赋值给原数组，原数组变为为{8，11，3，9，7，1，2，5}。
（3）是对下标[0,3]进行排序后合并
临时数组为：{3，7，9，11，0，0，0，0}，原数组为：{3，7，9，11，7，1，2，5}。
（4）是对下标[4,5]进行排序
临时数组为：{3，7，9，11，1，7，0，0}，原数组为：{3，7，9，11，1，7，2，5}。
（5）是对下标[6,7]进行排序
临时数组为：{3，7，9，11，1，7，2，5}，原数组为：{3，7，9，11，1，7，2，5}。
（6）是对下标[4,7]进行排序后合并
临时数组为：{3，7，9，11，1，2，5，7}，原数组为：{3，7，9，11，1，2，5，7}。
（6）是对下标[0,7]进行排序后合并
合并的思路如下图
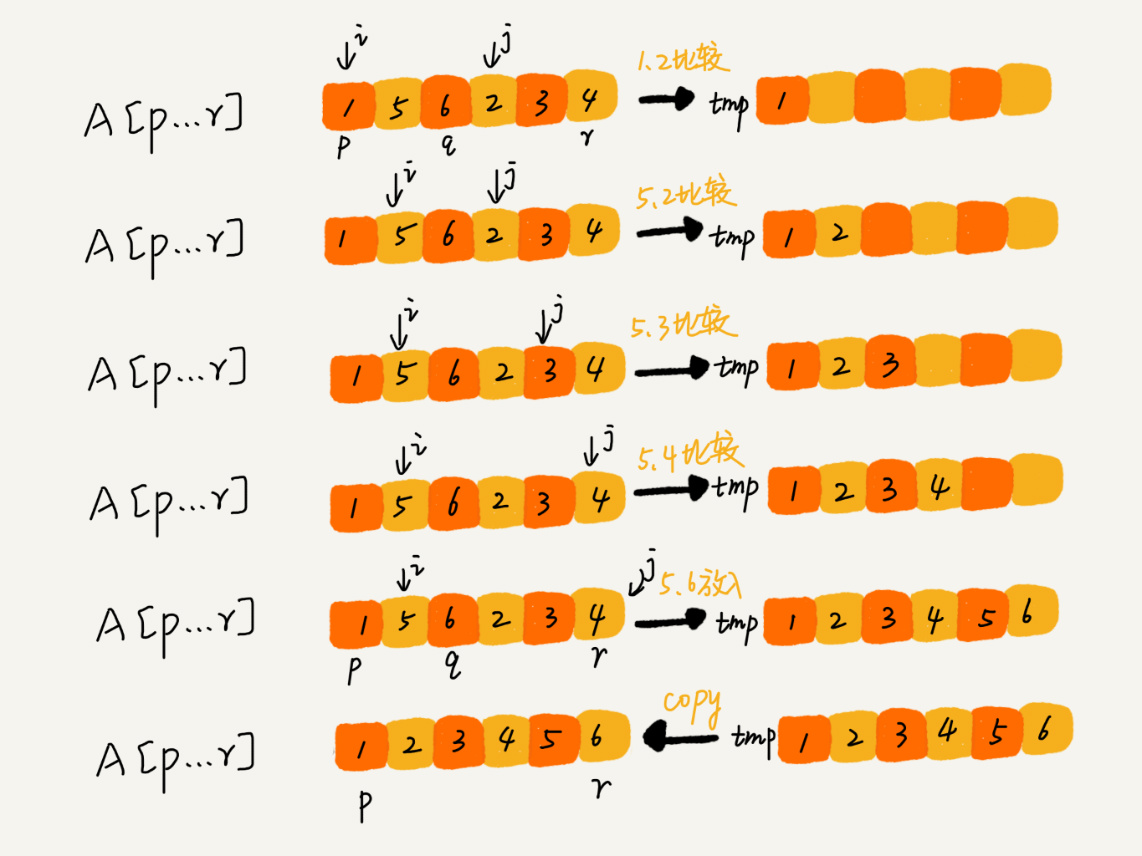
1、归并排序的代码
package mergesortdemo;
public class MergeSortDemo {
public static void main(String[] args) {
//我乱按的数组，我也不知道有几个元素
int[] MergeArray = {
4, 3, 2, 1};//, 55, 88, 33, 66, 54, 242, 432, 564, 756, 2342, 623, 856, 31};
printArray("排序前", MergeArray);
//排序方法
Mergesort(MergeArray);
printArray("排序后", MergeArray);
}
//打印方法
private static void printArray(String pre, int[] MergeArray) {
System.out.print(pre + "\n");
//完成排序后进行输出
for (int element : MergeArray) {
System.out.println(element);
}
}
//排序方法
public static void Mergesort(int[] array) {
System.out.println("开始排序");
Sort(array, 0, array.length - 1);
}
private static void Sort(int[] array, int left, int right) {
if (left >= right)
return;
int mid = (left + right) / 2;
//二路归并排序里面有两个Sort，多路归并排序里面写多个Sort就可以了
Sort(array, left, mid);
Sort(array, mid + 1, right);
merge(array, left, mid, right);
}
//合并数组
private static void merge(int[] MergeArray, int left, int mid, int right) {
int[] tmpArray = new int[MergeArray.length];
//
int ponitI = left;
int pointJ = mid + 1;
//拷贝索引
int pointCopy = left;
// 逐个归并
while (left <= mid && pointJ <= right) {
if (MergeArray[left] <= MergeArray[pointJ])
tmpArray[ponitI++] = MergeArray[left++];
else
tmpArray[ponitI++] = MergeArray[pointJ++];
}
// 将左边剩余的归并
while (left <= mid) {
tmpArray[ponitI++] = MergeArray[left++];
}
// 将右边剩余的归并
while (pointJ <= right) {
tmpArray[ponitI++] = MergeArray[pointJ++];
}
// TODO Auto-generated method stub
//从临时数组拷贝到原数组
while (pointCopy <= right) {
MergeArray[pointCopy] = tmpArray[pointCopy];
//输出中间归并排序结果
System.out.print(MergeArray[pointCopy] + "\t");
pointCopy++;
}
System.out.println();
}
}
代码的核心部分有两块
1.递归拆分原数组（非实际意义拆分，而是逻辑意义拆分）
private static void Sort(int[] array, int left, int right) {
if (left >= right){
return;
}
else {
int mid = (left + right) / 2;
//二路归并排序里面有两个Sort，多路归并排序里面写多个Sort就可以了
Sort(array, left, mid);
Sort(array, mid + 1, right);
merge(array, left, mid, right);
}
}
2.比较大小后，将值赋给临时数组，再通过临时数组将值赋给原数组。
//合并数组
private static void merge(int[] MergeArray, int left, int mid, int right) {
int[] tmpArray = new int[MergeArray.length];
//
int ponitI = left;
int pointJ = mid + 1;
//拷贝索引
int pointCopy = left;
// 逐个归并
while (left <= mid && pointJ <= right) {
if (MergeArray[left] <= MergeArray[pointJ])
tmpArray[ponitI++] = MergeArray[left++];
else
tmpArray[ponitI++] = MergeArray[pointJ++];
}
// 将左边剩余的归并
while (left <= mid) {
tmpArray[ponitI++] = MergeArray[left++];
}
// 将右边剩余的归并
while (pointJ <= right) {
tmpArray[ponitI++] = MergeArray[pointJ++];
}
//从临时数组拷贝到原数组
while (pointCopy <= right) {
MergeArray[pointCopy] = tmpArray[pointCopy];
//输出中间归并排序结果
System.out.print(MergeArray[pointCopy] + "\t");
pointCopy++;
}
System.out.println();
}
归并排序比较难理解的一点还是递归，明白递归的执行顺序，那么归并算法也就不难理解了。
2、归并排序是原地排序算法吗？
在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。
递归代码的空间复杂度并不能像时间复杂度那样累加。尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。
3、归并排序是稳定的排序算法吗？
在合并的过程中，如果元素值大小相同，是不会进行位置互换的，所以归并排序是一个稳定的排序算法。
4、归并排序的时间复杂度是多少？
归并排序涉及递归，时间复杂度的分析比较复杂，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。
五.快速排序（Quicksort，广泛应用，大数据量）
快速排序，简称快排。利用的也是分治思想，快排的分治思想是从数组中选择一个元素，作为分区点，从小到大排序，然后分区点循环对比其他的元素，小的放在分区点左边，大的放在分区点的右边。
循环利用这个方法，可以很快的进行排序，确实是很好的排序方法。
我看了好多人写的快速排序，思路各有不同。我觉得这个写的比较好，特别是他发的那几张图，认真看一下就能够更加深入的理解快速排序的思想。链接
我用我的理解大概的描述一下这个的思路，借一张图。
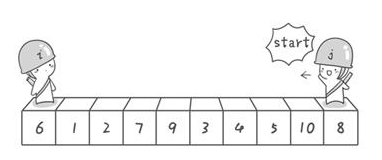
设置一个分区点，这个分区点可以随意设置。
假定设置的分区点为index(3)=7
分别有两个哨兵，从左右两端出发，右端先走，左端后走。
右端哨兵从右往左走，寻找比7小数字，然后停下来，会停在5上面。
左端哨兵从左往右出发，寻找比7大的数字，然后停下来，会停在9的上面。
然后为了避免增加空间复杂度，也为了避免进行数组位移操作，直接将7和5进行交换，交换后的数组就是{6,1,2,7,5,3,4,9,10,8}
然后右端哨兵再次出发，寻找比7小的数字，然后停下来，会停在4上面。
左端哨兵从左往右出发，寻找比7大的数字，但是从7到4一直没找到，会和右端哨兵相遇在4上，4比7小，于是4和7进行位置的交换，交换后的数组就是{6,1,2,4,5,3,7,9,10,8}，此时第一遍探测正式接数，比7大的都在7的右边，比7小的都在7的左边。
此时第一遍探测结束，数组被分为了逻辑的三个部分左端小于7，7，右端大于7。
左端部分再从中选择一个分区点，右端部分也选择一个分区点，此时数组是{6,1,2,4,5,3,7,9,10,8}。
假设左端选择分区点为1，右端选择分区点为9。然后根据递归算法的思想，先求{6，1，2，4，5，3}再求{9,10,8}的排序(此时并没有实际拆分数组，只是从逻辑上拆分了数组)
对{6，1，2，4，5，3}进行排序，分区点是1，哨兵从两端出发。
右端哨兵寻找比1小的数字，然后停下来，会停在1上面。
左端哨兵寻找比1大的数字，然后停下来，会停在6上面。
1和6进行交换得到{1，6，2，4，5，3}。
再次出发，最后两边都停在了1上。
对{9,10,8}进行排序，分区点是9，哨兵从两端出发。
右端哨兵寻找比9小的数字，然后停下来，会停在8上面。
左端哨兵寻找比9大的数字，然后停下来，会停在10上面。
交换得到{9，8，10}
右端哨兵在交换之后再次进行出发，停下来，会停在8上面。
左端哨兵寻找比9大的数字，但是没用，然后停下来，会停在8上面.。
交换最后落点8和分区点9得到{8，9，10}，这部分排序完毕
略
1、快速排序代码实现
package quicksortdemo;
//非随机快速排序。
public class QuickSortDemo {
public static void main(String[] args) {
int[] QuickSortArray = {
5, 4, 3, 2, 1, 55, 88, 33, 2, 4, 55, 75, 534, 66};
printArray("排序前", QuickSortArray);
System.out.println("开始排序");
QuickSort(QuickSortArray, 0, QuickSortArray.length - 1);
printArray("排序后", QuickSortArray);
}
//打印方法
private static void printArray(String pre, int[] MergeArray) {
System.out.print(pre + "\n");
//完成排序后进行输出
for (int element : MergeArray) {
System.out.println(element);
}
}
//这里是利用递归进行分组排序
private static void QuickSort(int[] QuickSortArray, int indexLeft, int indexRight) {
System.out.println("indexLeft :" + indexLeft);
System.out.println("indexRight :" + indexRight);
if (indexLeft >= indexRight) {
return;
}
int left = indexLeft;
int right = indexRight;
int temp = 0;
int randomIndex = left;// new Random().nextInt(right - left) + left;//随机选取点
System.out.println("randomIndex :" + randomIndex);
int randomPivot = QuickSortArray[randomIndex];
//条件是右端元素大于左端，即两端哨兵相遇时候终止。
while (left < right) {
//右侧哨兵从右向左寻找
//while循环，找到第一个符合条件点即退出当前循环
while (randomPivot <= QuickSortArray[right] && left < right) {
right--;
}
//左侧哨兵向右寻找
//while循环，找到第一个符合条件点即退出当前循环
while (randomPivot >= QuickSortArray[left] && left < right) {
left++;
}
//如果满足条件则交换
if (left < right) {
temp = QuickSortArray[right];
QuickSortArray[right] = QuickSortArray[left];
QuickSortArray[left] = temp;
}
}
//最后将两个哨兵相遇点和分区点进行交换。
QuickSortArray[indexLeft] = QuickSortArray[left];
QuickSortArray[left] = randomPivot;
//递归调用左半数组,
if (left > 0) {
QuickSort(QuickSortArray, indexLeft, left - 1);
}
if (right < indexRight) {
//递归调用右半数组
QuickSort(QuickSortArray, randomIndex + 1, indexRight);
}
}
}
2、快速排序是原地排序算法吗？
快苏排序并不需要额外开拓空间，所以是原地排序算法。
3、快速排序是稳定的排序算法吗？
快速排序在交换的过程中可能会有相同元素进行前后位置交换，所以不是稳定的个算法。
4、快速排序的时间复杂度是多少？
快排也是用递归来实现的，快排的时间复杂度也是 O(nlogn)。
六.桶排序（Bucket sort，先行排序）
桶排序，顾名思义，会用到“桶”，核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序（在桶内使用别的排序算法）之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。
桶排序是比较优秀的排序算法，但是有较为严苛的实现前置条件
首先，要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
其次，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了。
七.计数排序（Counting sort）
计数排序和桶排序的思路相似，区别在于计数排序对桶内的数据不进行排序，而是计数，计算桶内元素的个数。
计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。
记数排序有一个很巧妙地表示算法。
比如原数据是：2，5，3，0，2，3，0，3
从小到大进行排序后是0，0，2，2，3，3，3，5
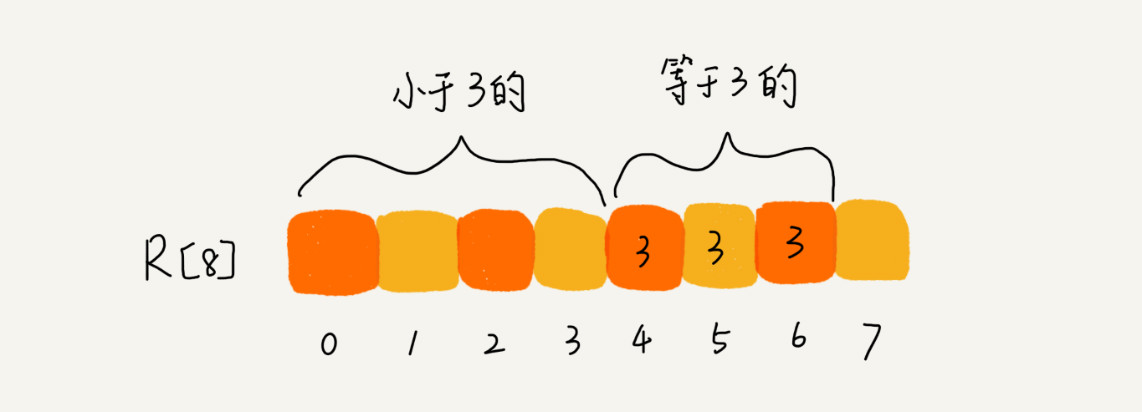也可以以这种形式进行表现
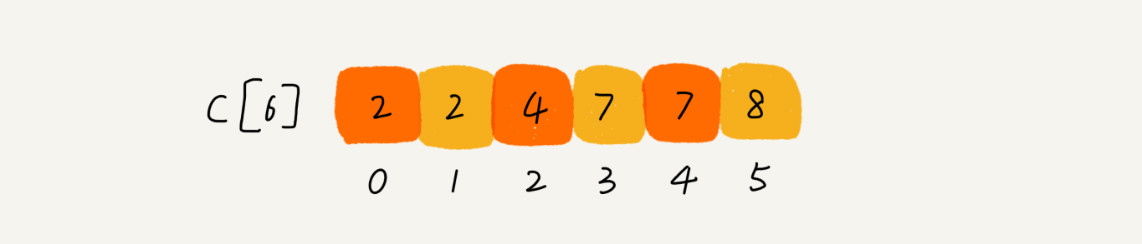
该数组内存储的不是具体的数据，而是该数据的个数。计数方法是对数组进行顺序求和，数组中C[INDEX]里的存储的是小于等于值INDEX的元素的个数，比如C[2]=4指的是小于等于2的元素有四个，C[3]=7表示小于等于3的元素个数有7个，相减就可以知道=3的个数有三个。
计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。
八.基数排序（Radix sort）
比如对手机号码或者身份证号进行排序，需要按照每一位进行排序，比如两个身份证A和B从小到大排序。如果A身份证的第一位号码已经比B大了，那么就直接拍为B,A,而不需要去比较AB后面的那些数据，等第一位数据排序完成之后，再进行第二位排序，这样的排序算法称之为基数排序。
对于长短不一的数据，可以将所有数据补齐到相同长度，长度不够的以0填充，因为根据ASCII 值，所有字母都大于“0”，所以补“0”不会影响到原有的大小顺序。这样就可以继续用基数排序了。
基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。
版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: