一、概述
PASS:我感觉很多东西都是基于不同数据结构实现的,所以我觉得我应该优先把这个看完,再去考虑学习别的进阶,我相信能够事半功倍。
复杂度分析我觉得是学习数据结构算法的基础,相当于程序的调试模式,要先会复杂度,才能考虑下一步的计划,我想多练习一些复杂度的分析,能够更快更好的掌握复杂度分析。
一.什么是复杂度分析?
1、 数据结构和算法解决是“如何让计算机更快时间、更省空间的解决问题”;
2、 因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能;
3、 分别用时间复杂度和空间复杂度两个概念来描述性能问题,二者统称为复杂度;
4、 复杂度描述的是算法执行时间(或占用空间)与数据规模的增长关系;
二.为什么要进行复杂度分析?
1、 和性能测试相比,复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点;
2、 掌握复杂度分析,将能编写出性能更优的代码,有利于降低系统开发和维护成本;
三.如何进行复杂度分析?
1、大O表示法
1)来源
算法的执行时间与每行代码的执行次数成正比,用T(n) = O(f(n))表示,其中T(n)表示算法执行总时间,f(n)表示每行代码执行总次数,而n往往表示数据的规模。
2)特点
以时间复杂度为例,由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势,所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响,所以在做时间复杂度分析时忽略这些项。
2、复杂度分析法则
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
四.常用的复杂度级别
多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n2)(平方阶)、O(n3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,
O(2^n)(指数阶)、O(n!)(阶乘阶)
二、时间复杂度分析
渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系
一.分析方法
1、关住执行次数最多的代码
只关注循环执行次数最多的一段代码,大 O 这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数,只需要记录一个最大阶的量级就可以了。所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。这段核心代码执行次数的 n 的量级,就是整段要分析代码的时间复杂度。
2、加法法则
总复杂度等于量级最大的那段代码的复杂度
3、乘法法则
嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
二.几种常见时间复杂度实例分析
1、O(1)
O(1) 只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。比如这段代码,即便有 3 行,它的时间复杂度也是 O(1),而不是 O(3)。
int i = 8;
int j = 6;
int sum = i + j;
2、O(logn)、O(nlogn)
复杂度为O(logn)
执行结果为

这里的n仅仅指的是循环给的值,并不是次数,次数为x,因此x=logn/log2,因此复杂度为O(logn)
i=1;
while (i <= N) {
i = i * 2;
}
3、O(m+n)、O(m*n)
代码的复杂度由两个数据的规模,这里无法确定m和n的大小,无法评估两个谁的量级比较大,因此不能简单地忽略。
int cal(int m, int n) {
int sum_1 = 0;//1
int i = 1;//2
for (; i < m; ++i) {
//3
sum_1 = sum_1 + i;//4
}
int sum_2 = 0;//5
int j = 1;//6
for (; j < n; ++j) {
//7
sum_2 = sum_2 + j;//8
}
return sum_1 + sum_2;//9
}
三.最好、最坏及平均情况时间复杂度分析
//原代码
// n表示数组array的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
}
}
return pos;
}
//优化后代码
// n表示数组array的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
代码分析:
在数组中查找变量x出现的位置,如果没有找到就返回-1
1、最好情况时间复杂度分析
在最理想的情况下,要查找的变量 x 正好是数组的第一个元素,这个时候对应的时间复杂度就是最好情况时间复杂度。
2、最坏情况时间复杂度分析
最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度。就像刚举的那个例子,如果数组中没有要查找的变量 x,我们需要把整个数组都遍历一遍才行,所以这种最糟糕情况下对应的时间复杂度就是最坏情况时间复杂度。
3、平均情况时间复杂度分析
最好情况时间复杂度和最坏情况时间复杂度对应的都是极端情况下的代码复杂度,发生的概率其实并不大。因此评估复杂度我觉得应该考虑的是平均情况时间复杂度,等同于期望平均复杂度。
前提条件
要查找的变量 x 在数组中的位置,需要一些假设条件
1、 假设元素在数组中与不在数组中的概率都为1/2;
2、 要查找的数据出现在0~n-1这n个位置的概率也是一样的,为1/n;
在数组中:1/2*(1/n+2/n+3/n+…+n/n)=在数组中的概率遍历需要的时间
+
不在数组中:1/2n=不在数组中的概率*遍历需要的时间
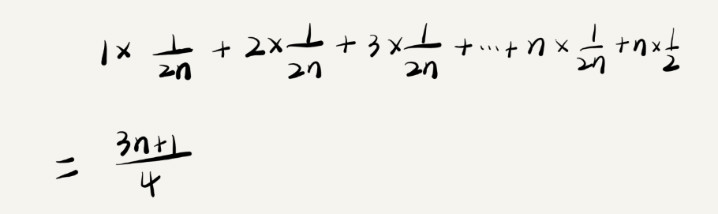
4、均摊时间复杂度分析(平摊分析)
均摊时间复杂度=特殊的平均情况时间复杂度
这段代码的复杂度跟阶段性相关(代码看了半天…太久没做过题,分段讨论都忘了)
1、 当循环i小于数组长度的时候,for循环不会进入,那么复杂度就是O(1);
2、 当i=n的时候,进入了for循环,只有这一次的循环时间复杂度是O(n);
最好情况时间复杂度分析:O(1)
最坏情况时间复杂度分析:O(n)
平均情况时间复杂度分析:分为N+1中只有1种复杂度是N其他1-N的复杂度都是1
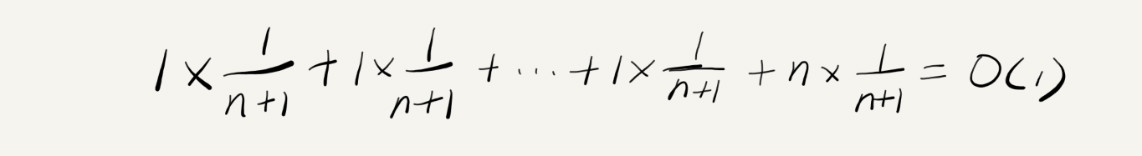
出现O(1)的次数远大于出现O(n)出现的次数,那么平均平摊时间复杂度就是O(1)
// array表示一个长度为n的数组
// 代码中的array.length就等于n
int[] array = new int[n];
int count = 0;
void insert(int val) {
if (count == array.length) {
int sum = 0;//初始化求和值
for (int i = 0; i < array.length; ++i) {
//遍历求和
sum = sum + array[i];//数组求和
}
array[0] = sum;//给数组赋值
count = 1;
}
array[count] = val;
++count;
}
三、空间复杂度分析
表示算法的存储空间与数据规模之间的增长关系。
除了第2行申请了一个大小为N的int类型数组,其他代码没有占用更多的空间,因此整段代码的复杂度是O(n)
void print(int n) {
int i = 0;//1
int[] a = new int[n];//2
for (i; i <n; ++i) {
//3
a[i] = i * i;//4
}
for (i = n-1; i >= 0; --i) {
//5
print out a[i]//6
}
}
空间和时间不同,重复的去申请空间会消耗系统资源,正常人没人会这么干,如果能预估到数据大小,最好是初始化的时候一次申请。
四、复杂度代码案例分析
1、代码分析(1)
int cal(int n) {
//1
int sum = 0;//2
int i = 1;//3
for (; i <= n; ++i) {
//4
sum = sum + i;//5
}//6
return sum;//7
}
分析:
从CPU 的角度来看,这段代码的每一行都执行着类似的操作:读数据-运算-写数据。尽管每行代码对应的 CPU 执行的个数、执行的时间都不一样,但是,我们这里只是粗略估计,所以可以假设每行代码执行的时间都一样,为 unit_time(单位时间)。
第2、3 行代码分别需要 1 个 unit_time 的执行时间,第 4、5 行都运行了 n 遍,所以需要 2n*unit_time 的执行时间,所以这段代码总的执行时间就是 (2n+2)*unit_time。
T(n) = O(2n+2),当n无穷大的时候,低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。
因此这段代码的复杂度是O(n)
2、代码分析(2)
int cal(int n) {
//1
int sum = 0;//2
int i = 1;//3
int j = 1;//4
for (; i <= n; ++i) {
//5
j = 1;//6
for (; j <= n; ++j) {
//7
sum = sum + i * j;//8
}
}
}
分析:
第2,3,4行代码,每行都需要一个单位时间,第5,6行代码执行了n遍,需要2n个单位时间,第7,8行执行了2nn遍,因此需要2n^2,因此
T(N)=2n^2+2n+3,当n无穷大的时候,低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。
因此这段代码的复杂度是O(n^2)
3、代码分析(选择排序)
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] n = new int[]{
1,6,3,8,33,27,66,9,7,88};
int temp,index = -1;
for (int i = 0; i < n.length-1; i++) {
index=i;
//如果大于,暂存较小的数的下标
for (int j = i+1; j <n.length; j++) {
if(n[index]>n[j]){
index = j;
}
}
将一趟下来求出的最小数,与这个数交换
if(index>0){
temp = n[i];
n[i] = n[index];
n[index] = temp;
}
System.out.println(Arrays.toString(n));
}
System.out.println(Arrays.toString(n));
}
}
4、代码分析(冒泡排序)
import java.util.Arrays;
public class 冒泡 {
public static void main(String[] args) {
int[] n = new int[]{
1,6,3,8,33,27,66,9,7,88};
int temp;
for (int i = 0; i < n.length-1; i++) {
for (int j = 0; j <n.length-1; j++) {
if(n[j]>n[j+1]){
temp = n[j];
n[j] = n[j+1];
n[j+1] = temp;
}
}
}
System.out.println(Arrays.toString(n));
}
}
5、代码分析(直接插入排序)
import java.util.Arrays;
public class insertSort {
public static void main(String[] args) {
int[] n = new int[]{
20,12,15,1,5,49,58,24,578,211,20,214,78,35,125,789,11};
int temp = 0,j;
for (int i = 1; i < n.length; i++) {
temp = n[i];
for (j = i; j >0; j--) {
//如果当前数前面的数大于当前数,则把前面的数向后移一个位置
if(n[j-1]>temp){
n[j] = n[j-1];
//第一个数已经移到第二个数,将当前数放到第一个位置,这一趟结束
if(j==1){
n[j-1] = temp;
break;
}
}else{
//如果不大于,将当前数放到j的位置,这一趟结束
n[j] = temp;
break;
}
}
System.out.println(Arrays.toString(n));
}
System.out.println(Arrays.toString(n));
}
}
6、代码分析(快速排序)
import java.util.Arrays;
public class insertSort {
public static void main(String[] args) {
int[] n = new int[]{
20,12,15,1,5,49,58,24,578,211,20,214,78,35,125,789,11};
int temp = 0,j;
for (int i = 1; i < n.length; i++) {
temp = n[i];
for (j = i; j >0; j--) {
//如果当前数前面的数大于当前数,则把前面的数向后移一个位置
if(n[j-1]>temp){
n[j] = n[j-1];
//第一个数已经移到第二个数,将当前数放到第一个位置,这一趟结束
if(j==1){
n[j-1] = temp;
break;
}
}else{
//如果不大于,将当前数放到j的位置,这一趟结束
n[j] = temp;
break;
}
}
System.out.println(Arrays.toString(n));
}
System.out.println(Arrays.toString(n));
}
}
7、代码分析(归并排序)
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{
3,6,4,7,5,2};
merge(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
//归并
public static void merge(int[] arr,int low,int high){
int center = (high+low)/2;
if(low<high){
//递归,直到low==high,也就是数组已不能再分了,
merge(arr,low,center);
merge(arr,center+1,high);
//当数组不能再分,开始归并排序
mergeSort(arr,low,center,high);
System.out.println(Arrays.toString(arr));
}
}
//排序
public static void mergeSort(int[] arr,int low,int center,int high){
//用于暂存排序后的数组的临时数组
int[] tempArr = new int[arr.length];
int i = low,j = center+1;
//临时数组的下标
int index = 0;
//循环遍历两个数组的数字,将小的插入到临时数组里
while(i<=center && j<= high){
//左边数组的数小,插入到新数组
if(arr[i]<arr[j]){
tempArr[index] = arr[i];
i++;
}else{
//右边数组的数小,插入到新数组
tempArr[index] = arr[j];
j++;
}
index++;
}
//处理左半边数组多余的数据,将左半边多余的数据直接追加的临时数组的后面
while(i<=center){
tempArr[index] = arr[i];
i++;
index++;
}
//处理右半边数组多余的数据,将右半边多余的数据直接追加的临时数组的后面
while(j<= high){
tempArr[index] = arr[j];
j++;
index++;
}
//将临时数组中的数据重新放进原数组
for (int k = 0; k < index; k++) {
arr[k+low] = tempArr[k];
}
}
}
8、代码分析(基数排序)
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{
10,6,3,8,33,27,66,9,7,88};
radixSort(arr);
}
private static void radixSort(int[] arr) {
//求出待排数的最大数
int maxLength=0;
for (int i = 0; i < arr.length; i++) {
if(maxLength<arr[i])
maxLength = arr[i];
}
//根据最大数求最大长度
maxLength = (maxLength+"").length();
//用于暂存数据的数组
int[][] temp = new int[10][arr.length];
//用于记录temp数组中每个桶内存的数据的数量
int[] counts = new int[10];
//用于记录每个数的i位数
int num = 0;
//用于取的元素需要放的位置
int index = 0;
//根据最大长度决定排序的次数
for (int i = 0,n=1; i < maxLength; i++,n*=10) {
for (int j = 0; j < arr.length; j++) {
num = arr[j]/n%10;
temp[num][counts[num]] = arr[j];
counts[num]++;
}
//从temp中取元素重新放到arr数组中
for (int j = 0; j < counts.length; j++) {
for (int j2 = 0; j2 < counts[j]; j2++) {
arr[index] = temp[j][j2];
index++;
}
counts[j]=0;
}
index=0;
}
System.out.println(Arrays.toString(arr));
}
}
9、代码分析( 希尔(shell)排序)
import java.util.Arrays;
public class shell {
public static void main(String[] args) {
int[] arr = new int[]{
10,6,3,8,33,27,66,9,7,88};
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
private static void shellSort(int[] arr) {
int temp;
//控制增量序列,增量序列为1的时候为最后一趟
for (int i = arr.length/2; i >0; i/=2) {
//根据增量序列,找到每组比较序列的最后一个数的位置
for (int j = i; j < arr.length; j++) {
//根据该比较序列的最后一个数的位置,依次向前执行插入排序
for (int k = j-i; k >=0; k-=i) {
if(arr[k]>arr[k+i]){
temp = arr[k];
arr[k] = arr[k+i];
arr[k+i] = temp;
}
}
}
}
}
}
10、代码分析(堆排序)
import java.util.Arrays;
public class duipaixu {
public static void main(String[] args) {
int[] arr = new int[]{
4,6,8,5,9};
int length = arr.length;
//从最后一个非叶节点开始构建大顶堆
for (int i = arr.length/2-1; i >=0; i--) {
maximumHeap(i,arr,length);
}
//从最小的叶子节点开始与根节点进行交换并重新构建大顶堆
for (int i = arr.length-1; i >=0; i--) {
// System.out.println(Arrays.toString(arr));
swap(arr,0,i);
length--;
maximumHeap(0,arr,length);
}
System.out.println(Arrays.toString(arr));
}
//构建大顶堆
public static void maximumHeap(int i,int[] arr,int length){
int temp = arr[i];
for (int j = i*2+1; j < length; j=j*2+1) {
//如果右孩子大于做孩子,则指向右孩子
if(j+1<length && arr[j+1]>arr[j]){
j++;
}
//如果最大的孩子大于当前节点,则将大孩子赋给当前节点,修改当前节点为其大孩子节点,再向下走。
if(arr[j]>temp){
arr[i] = arr[j];
i = j;
}else{
break;
}
}
//将temp放到最终位置
arr[i] = temp;
}
//交换
public static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
11、代码分析(11)
decimal Factorial(int n)
{
if (n == 0)
return 1;
else
return n * Factorial(n - 1);
}
12、代码分析(12)
long FindInversions(int[] array)
{
long inversions = 0;
for (int i = 0; i < array.Length; i++)
for (int j = i + 1; j < array.Length; j++)
if (array[i] > array[j])
inversions++;
return inversions;
}
13、代码分析(13)
long SumMN(int n, int m)
{
long sum = 0;
for (int x = 0; x < n; x++)
for (int y = 0; y < m; y++)
sum += x * y;
return sum;
}
14、代码分析(14)
decimal Sum3(int n)
{
decimal sum = 0;
for (int a = 0; a < n; a++)
for (int b = 0; b < n; b++)
for (int c = 0; c < n; c++)
sum += a * b * c;
return sum;
}
15、代码分析(15)
public static boolean contains(int[] haystack, int needle) {
// haystack 是否包含 needle?
for (int n : haystack) {
if (n == needle) {
return true;
}
}
return false;
}
16、代码分析(16)
public static void printAllNumbersThenAllPairSums(int[] numbers) {
System.out.println("these are the numbers:");
for (int number : numbers) {
System.out.println(number);
}
System.out.println("and these are their sums:");
for (int firstNumber : numbers) {
for (int secondNumber : numbers) {
System.out.println(firstNumber + secondNumber);
}
}
}
17、代码分析(17
// 全局变量,大小为10的数组array,长度len,下标i。
int array[] = new int[10];
int len = 10;
int i = 0;
// 往数组中添加一个元素
void add(int element) {
if (i >= len) {
// 数组空间不够了
// 重新申请一个2倍大小的数组空间
int new_array[] = new int[len*2];
// 把原来array数组中的数据依次copy到new_array
for (int j = 0; j < len; ++j) {
new_array[j] = array[j];
}
// new_array复制给array,array现在大小就是2倍len了
array = new_array;
len = 2 * len;
}
// 将element放到下标为i的位置,下标i加一
array[i] = element;
++i;
}
18、代码分析(18)
19、代码分析(19)
20、代码分析(20)
21、代码分析(21)
22、代码分析(22)
参考:
1、数据结构与算法之美
2、[八大排序算法详解(动图演示 思路分析 实例代码java 复杂度分析 适用场景)][_ _java _]
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: