数据结构与算法之美-03 |数组

一、定义

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。
数组长度一旦声明,不可改变不可追加，根据数组的维度，可以将其分为一维数组、二维数组和多维数组等。

一.数组定义中的关键词

1、线性表

线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组，链表、队列、栈等也是线性表结构。

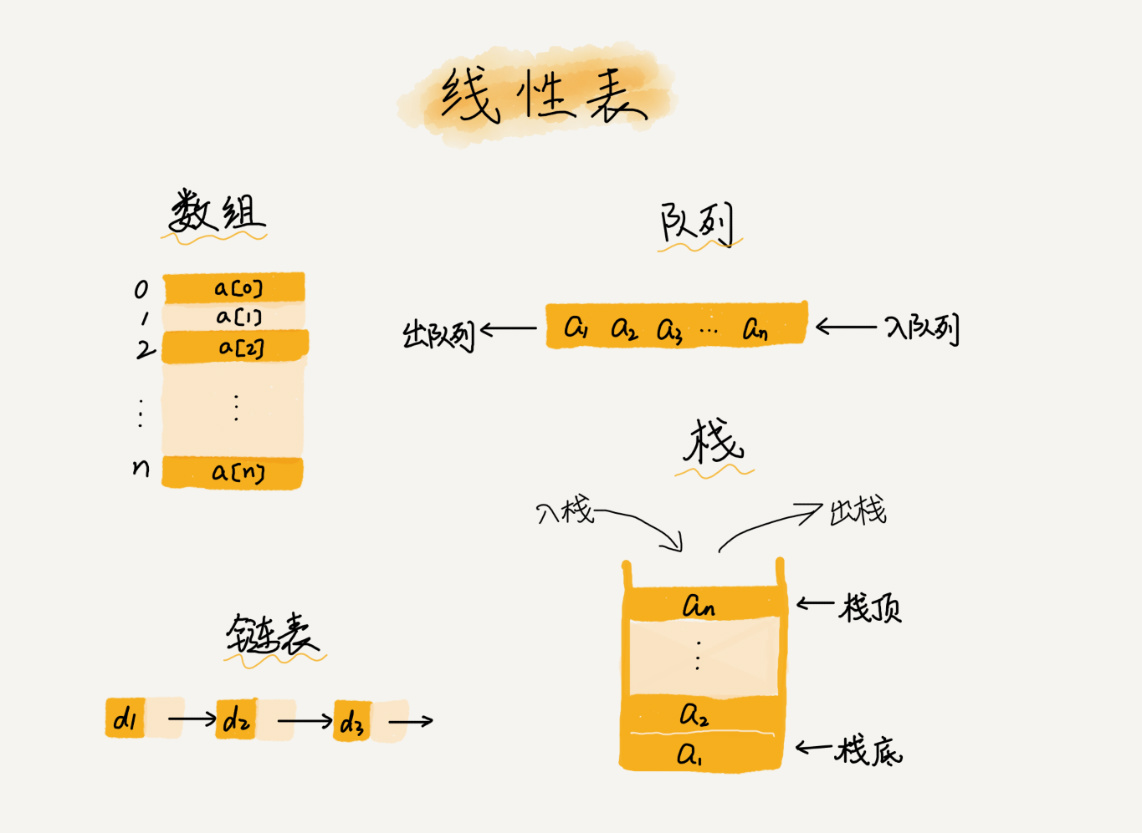
非线性表就指的是二叉树，堆，图等，为什么叫非线性，是因为在非线性表结构中，数据之间不只是简单的前后关系。

2、连续的内存空间和相同类型的数据

正是因为这两个限制，它才有了一个堪称“杀手锏”的特性：“随机访问”。但有利就有弊，这两个限制也让数组的很多操作变得非常低效，比如要想在数组中删除、插入一个数据，为了保证连续性，就需要做大量的数据搬移工作。

2.1连续内存空间

当创建一个数组时，计算机会在内存开辟一个空间，并给该数组一个地址值，数组内的元素查询方式如下：

a[k]_address = base_address + k * type_size

2.2低效的“插入”和“删除”

(1).插入

假设数组的长度为 n，将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾出来，给新来的数据，我们需要将第 k～n 这部分的元素都顺序地往后挪一位。
如果在数组的末尾插入元素，那就不需要移动数据了，这时的时间复杂度为 O(1)。但如果在数组的开头插入元素，那所有的数据都需要依次往后移动一位，所以最坏时间复杂度是 O(n)。在每个位置插入元素的概率是一样的，所以平均情况时间复杂度为 (1+2+…n)/n=O(n)。

如果该数组元素没有顺序（元素的下标有顺序，值没有顺序），只是当作一个集合使用。
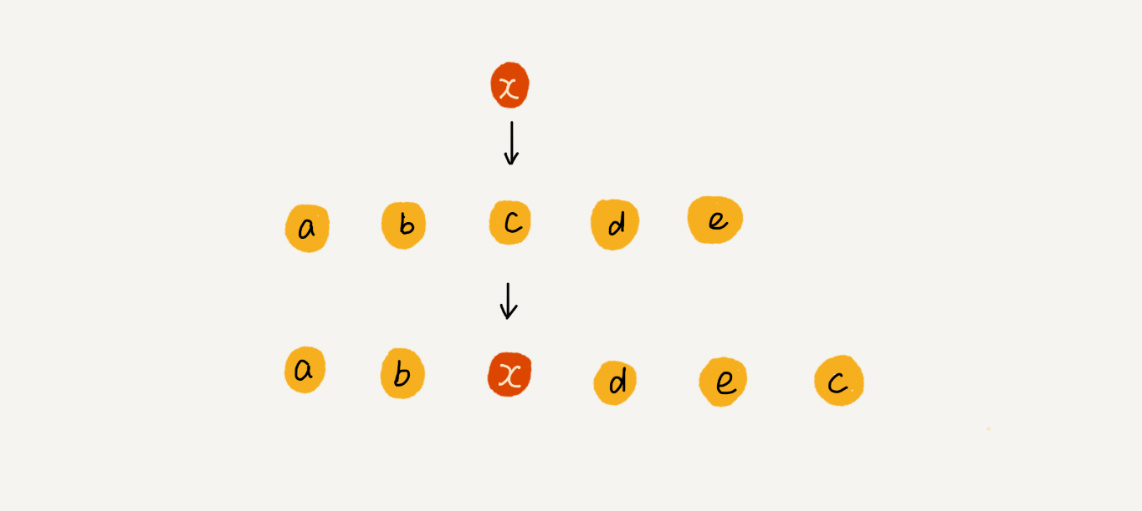
如果在给A、B、C、D、E中的下表为3的地方插入一个数据X。
有两种算法
1、将X插入ABCDE中，得到ABXCDE，将CDE向后移动了一个位置；
2、将C追加到数组末尾，将C的值替换为X，这样之操作了一个元素，极大地提高了运行效率（快速排序思想）；

(2).删除

和插入类似，如果删除数组末尾的数据，则最好情况时间复杂度为 O(1)；如果删除开头的数据，则最坏情况时间复杂度为 O(n)；平均情况时间复杂度也为 O(n)。
在实际操作中，如果把多次删除操作集中在一起执行，那么删除效率会提升。

数组a[10]中存储了 8 个元素：a，b，c，d，e，f，g，h。现在，我们要依次删除 a，b，c 三个元素。

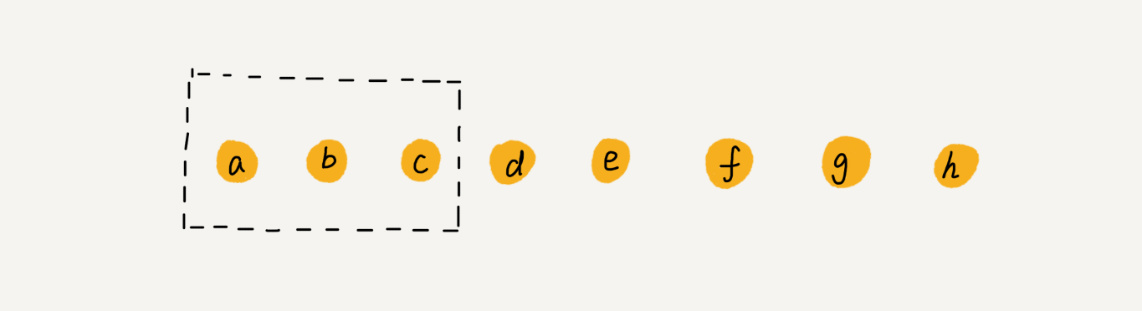
为了避免 d，e，f，g，h 这几个数据会被搬移三次，可以先记录下已经删除的数据。每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。（JVM 标记清除垃圾回收算法）

二、使用数组还是容器

容器的底层结构也是数组，容器最大的优势就是将很多数组操作的细节封装起来。比如数组插入、删除数据时需要搬移其他数据等。另外，它还有一个优势，就是支持动态扩容。
数组本身在定义的时候需要预先指定大小，因为需要分配连续的内存空间。数组一旦确定就不可变，如果想要扩容变大，只能申请新的数组，将原来的数组赋值过去，然后再将新的数据插入。
但是使用容器，就不需要考虑扩容问题（实际上也是申请了新的空间，只不过是自动进行了，会默认扩容为原来的1.5倍），但是扩容操作涉及内存申请和数据搬移，是比较耗时的。所以，如果事先能确定需要存储的数据大小，最好在创建 ArrayList 的时候事先指定数据大小。
容器无法存储基本类型数据，会进行装箱和拆箱，装箱拆箱过程会有一定的性能损耗。
如果特别在意性能建议使用数组，一般情况下，容器就可以了。